题目内容
11．已知数列{an}满足：a1=3232，an=2-1an−11an−1（n≥2）（1）若bn=1an−11an−1，证明：{bn}为等差数列；
（2）若cn=4an−14an−1-5，Sn为{cn}的前n项和，求证：1S1−11S1−1+1S2−11S2−1+…+1Sn−11Sn−1＜73907390．
分析 （1）易得an+1an=2an-1，从而bn+1-bn=1an+1−11an+1−1-1an−11an−1，化简得bn+1-bn=1，故数列{bn}为首项为2、公差为1的等差数列；
（2）数列{bn}的前n项和Tn=2n+n（n−1）22n+n（n−1）2=n2+3n2n2+3n2，则Sn=4Tn-5n=4×n2+3n2n2+3n2-5n=2n2+n，将1Sn−11Sn−1放大至12（1n−1−1n）12（1n−1−1n），再将1S1−11S1−1+1S2−11S2−1+…+1Sn−11Sn−1中第6项以后放缩即可．
解答 证明：由an=2-1an−11an−1可知anan-1=2an-1-1，所以an+1an=2an-1．
（1）∵bn=1an−11an−1，
∴bn+1-bn=1an+1−11an+1−1-1an−11an−1
=an−1−an+1+1（an+1−1）（an−1）an−1−an+1+1（an+1−1）（an−1）
=an−an+1anan+1−an−an+1+1an−an+1anan+1−an−an+1+1
=an−an+12an−1−an−an+1+1an−an+12an−1−an−an+1+1
=1，
又b1=1a1−1b1=1a1−1=132−1132−1=2，
故数列{bn}为首项为2、公差为1的等差数列；
（2）由（1）知，数列{bn}的前n项和Tn为：
Tn=2n+n（n−1）22n+n（n−1）2=n2+3n2，
又cn=4an−1-5，
所以{cn}的前n项和Sn为：
Sn=4Tn-5n=4×n2+3n2-5n=2n2+n，
则1Sn−1=12n2+n−1=1（2n−1）（n+1）
又2n2+n-1＞2n2-2n=2n（n-1）
所以1Sn−1＜12（1n−1−1n），
所以1S1−1+1S2−1+…+1Sn−1
＜11×2+13×3+15×4+17×5+19×6+12[15-16+…+1n−1-1n]
＜12+19+120+135+154+110
=3055037800＜7390，
即1S1−1+1S2−1+…+1Sn−1＜7390．
点评 本题考查了递推式的应用、“裂项求和”以及放缩法，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
，若函数
，有大于零的极值点，则（ ）
B．
D．
，下列命题正确的是 .
关于原点
中心对称；
，
两不同的点为切点作两条互相平行的切线，分别与
交于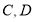
两点，则这四个点的横坐标满足关系
；
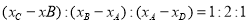为切点，作切线与
，再以点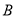
为切点作直线与
，再以点
作切点作直线与
，则
点横坐标为
；
，函数
，使得以它们为顶点的四边形有且仅有一个正方形.