题目内容
过抛物线y2=2x内的任意一点Q(s,t)(t2<2s)作两条相互垂直的弦AB,CD,若弦AB,CD的中点分别为M,N,直线MN恒过定点( )A.(s+1,0)
B.(|1-s|,0)
C.(1+2s,0)
D.(|1-2s|,0)
【答案】分析:本选择题为了简化计算,不妨取Q点是抛物线的焦点( ,0).若要证直线MN必过定点P,只需求出含参数的直线MN的方程,观察是否过定点即可.因此设出A、B、M、N的坐标,用A、B坐标表示M、N坐标,从而求出直线MN方程,即可得直线必过定点,从而得出正确选项.
,0).若要证直线MN必过定点P,只需求出含参数的直线MN的方程,观察是否过定点即可.因此设出A、B、M、N的坐标,用A、B坐标表示M、N坐标,从而求出直线MN方程,即可得直线必过定点,从而得出正确选项.
解答:解:不妨取Q点是抛物线的焦点( ,0).
,0).
设点A(x1,y1),B(x2,y2),M(x3,y3),N(x4,y4)
把直线AB:y=k(x- )代入y2=2x,得
)代入y2=2x,得
k2x2-(k2+2)x+ k2=0,
k2=0,
∴x3=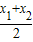 =
= +
+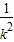 ,y3=k(x3-
,y3=k(x3- )=
)=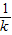
同理可得,x4= +k2,y4=-k,
+k2,y4=-k,
∴kMN=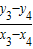 =
=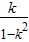
∴直线MN为y-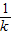 =
=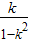 (x-
(x- -
-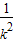 ),即y=
),即y=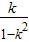 (x-
(x- ),
),
结合直线方程的点斜式,可得直线恒过定点P( ,0),
,0),
对照Q点是抛物线的焦点( ,0),定点P可以写成(
,0),定点P可以写成( +1,0).
+1,0).
故选A.
点评:本题给出抛物线互相垂直的弦AB、CD,求它们的中点确定的直线恒过定点.着重考查了直线与抛物线位置关系、直线过定点的判断等知识,属于中档题.
 ,0).若要证直线MN必过定点P,只需求出含参数的直线MN的方程,观察是否过定点即可.因此设出A、B、M、N的坐标,用A、B坐标表示M、N坐标,从而求出直线MN方程,即可得直线必过定点,从而得出正确选项.
,0).若要证直线MN必过定点P,只需求出含参数的直线MN的方程,观察是否过定点即可.因此设出A、B、M、N的坐标,用A、B坐标表示M、N坐标,从而求出直线MN方程,即可得直线必过定点,从而得出正确选项.解答:解:不妨取Q点是抛物线的焦点(
 ,0).
,0).设点A(x1,y1),B(x2,y2),M(x3,y3),N(x4,y4)
把直线AB:y=k(x-
 )代入y2=2x,得
)代入y2=2x,得k2x2-(k2+2)x+
 k2=0,
k2=0,∴x3=
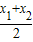 =
= +
+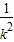 ,y3=k(x3-
,y3=k(x3- )=
)=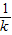
同理可得,x4=
 +k2,y4=-k,
+k2,y4=-k,∴kMN=
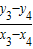 =
=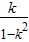
∴直线MN为y-
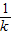 =
=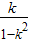 (x-
(x- -
-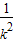 ),即y=
),即y=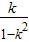 (x-
(x- ),
),结合直线方程的点斜式,可得直线恒过定点P(
 ,0),
,0),对照Q点是抛物线的焦点(
 ,0),定点P可以写成(
,0),定点P可以写成( +1,0).
+1,0).故选A.
点评:本题给出抛物线互相垂直的弦AB、CD,求它们的中点确定的直线恒过定点.着重考查了直线与抛物线位置关系、直线过定点的判断等知识,属于中档题.

练习册系列答案
相关题目