Question

如图1-4-6，在△ABC中，CD⊥AB于D，DE⊥AC于E，DF⊥BC于F，求证:△CEF∽△CBA.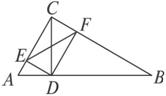

图1-4-6

Answer 1

思路分析：要证明△CEF∽△CBA，题设中已具备了∠BCA=∠ECF，再找出一对角相等就不太容易了，因此，考虑证明∠BCA与∠ECF的夹边成比例，即，即证CE·CA=CF·CB，再从已知条件出发考虑问题，在Rt△ADC中，DE⊥AC，根据定理能推出CD²=CE·CA，同理可得CD²=CF·CB,这样，CE·CA=CF·CB，问题就能得证.

证明：∵△ADC是直角三角形，DE⊥AC，∴CD²=CE·CA.

同理，可得CD²=CF·CB.∴CE·CA=CF·CB,即.

又∵∠BCA=∠ECF，∴△CEF∽△CBA.

    深化升华 当题目中缺少角相等时，应该考虑利用相等的角的两边对应成比例，即及时转换解题思路，而不能只想到找两对角相等，因为我们还有其他的判定定理.