题目内容
【题目】已知椭圆
：
的离心率
，左、右焦点分别为
、
，抛物线
的焦点
恰好是该椭圆的一个顶点.
（1）求椭圆的方程；
（2）已知直线
：
与圆
：
相切，且直线与椭圆相交于
、
两点，求
的值.
【答案】（1）
；（2）0
【解析】
（1）由抛物线
的焦点
是该椭圆的一个顶点，可得
，结合离心率
，可求
，进而可求出
，从而可求椭圆的方程.
（2）由直线和圆相切，可知圆心到直线的距离等于半径，即
，设
，
，联立直线和圆的方程，整理后由韦达定理可知，
，
，从而可求
.
解：（1）因为椭圆
的离心率，所以
，即
．
因为抛物线的焦点恰好是该椭圆的一个顶点，所以，
所以
，则
，所以椭圆的方程为．
（2）由圆的方程可知，圆心为
，半径为
；由于直线
与圆
相切，
故圆心到直线的距离
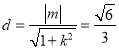，整理得，
则联立直线和椭圆的方程，即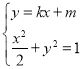
，消去
，得
，设，，则
，，则
．
所以
.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某市房产中心数据研究显示，2018年该市新建住宅销售均价如下表.3月至7月房价上涨过快，为抑制房价过快上涨，政府从8月份开始出台了相关限购政策，10月份开始房价得到了很好的抑制.
均价（万元/ | 0.95 | 0.98 | 1.11 | 1.12 | 1.20 | 1.22 | 1.32 | 1.34 | 1.16 | 1.06 |
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
（Ⅰ）请建立3月至7月线性回归模型（保留小数点后3位），并预测若政府不宏观调控，12月份该市新建住宅销售均价；
（Ⅱ）试用相关系数说明3月至7月各月均价
（万元/
）与月份
之间可用线性回归模型（保留小数点后2位）
参考数据：
，
，
，
，
回归方程斜率和截距最小二乘法估计公式
；
相关系数
.
