题目内容

若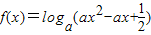在[1，]上恒正，则实数a的取值范围是    ．
【答案】分析：对底数进行分类讨论，将对数值恒正，转化为真数与1的比较，由此可求实数a的取值范围．
解答：解：若a＞1，则问题等价于＞0在[1，]上恒成立，
因为对于的二次函数在[1，]上单调递增，所以＞0，不成立；
若0＜a＜1，则问题等价于＜0，且在[1，]上恒成立，
因为对于的二次函数在[1，]上单调递增，
所以，解得a＜；
函数在[1，]上单调递增，所以1-1+＞0成立，
综上，0＜a＜
故实数a的取值范围是
故答案为：
点评：本题考查对数函数的性质，考查分类讨论的数学思想，考查学生分析转化问题的能力，属于中档题．
练习册系列答案
相关题目
设函数f(x)=
log
1-mx
x-1
a
为奇函数，g（x）=f（x）+loga（x-1）（ax+1）（ a＞1，且m≠1）．
（1）求m值；
（2）求g（x）的定义域；
（3）若g（x）在[-
5
2
，-
3
2
]上恒正，求a的取值范围．
若f(x)=loga(ax2-ax+
1
2
)在[1，
3
2
]上恒正，则实数a的取值范围是
(0，
2
3
)
(0，
2
3
)
．
设函数f(x)=
1og
1-mx
x-1
a
为奇函数，g（x）=f（x）+loga（x-1）（ax+1）（ a＞1，且m≠1）．
（1）求m值；
（2）求g（x）的定义域；
（3）若g（x）在[-
5
2
，-
3
2
]上恒正，求a的取值范围．
若f(x)=loga(ax2-ax+
1
2
)在[1，
3
2
]上恒正，则实数a的取值范围是______．

 （满分１５分）已知.

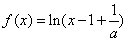（1）设F（x）=f(x) m+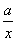，其中a>0．求F(x)的单调区间；

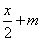（2）当a=1时，若对于任意正实数b，关于x不等式bf(x)>，在[1，e]上恒成立，求实数m的取值范围．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网