Question

 （满分１５分）已知.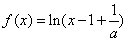

（1）设F（x）=f(x) m+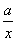，其中a>0．求F(x)的单调区间；

（2）当a=1时，若对于任意正实数b，关于x不等式bf(x)>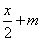，在[1，e]上恒成立，求实数m的取值范围．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

 （1）F（x）=

      F^/（x）=

      当a>2时，F(x)增区间（1，1），（a1，+），减区间（1，a1）

当a=2时，F(x)增区间（）

当1<a<2时，F(x)增区间，减区间（a1,1）

当a=1时，F(x)增区间（），减区间（0，1）

当0<a<1时，F(x)增区间（），（1，+），减区间（a1,0），（0，1）

（2）

当x=1时，       ∴

当1<x≤e时,0<lnx≤1

∴对成立

∴       ∴

∴成立

∴

综上所述，