题目内容
已知函数 .
.
(1)求 的值及函数
的值及函数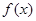 的单调递增区间;
的单调递增区间;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
 .
.(1)求
 的值及函数
的值及函数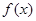 的单调递增区间;
的单调递增区间;(2)求函数
 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.(1) ,
,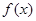 的单调递增区间是
的单调递增区间是 ,
, ;(2)
;(2)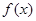 取得最小值
取得最小值 ,
,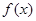 取得最大值
取得最大值 .
.
 ,
,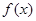 的单调递增区间是
的单调递增区间是 ,
, ;(2)
;(2)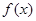 取得最小值
取得最小值 ,
,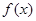 取得最大值
取得最大值 .
.试题分析:(1)求
 的值及函数
的值及函数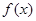 的单调递增区间,首先对函数
的单调递增区间,首先对函数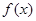 进行化简,将他化为一个角的一个三角函数,由已知
进行化简,将他化为一个角的一个三角函数,由已知 ,可用二倍角公式将函数
,可用二倍角公式将函数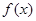 化为
化为 ,即可求出
,即可求出 的值及函数
的值及函数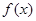 的单调递增区间;(2)求函数
的单调递增区间;(2)求函数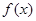 在
在 上的最大值和最小值,由(1)知
上的最大值和最小值,由(1)知 ,由
,由 得,
得, ,可利用
,可利用 的图像可得,函数
的图像可得,函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.试题解析:(1)因为

所以,
 .
.由
 ,
, ,
,得
 ,
,
所以
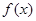 的单调递增区间是
的单调递增区间是 ,
, . 8分
. 8分(2)因为
 所以
所以 .
.所以,当
 ,即
,即 时,
时,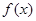 取得最小值
取得最小值 ;
;当
 即
即 时,
时,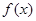 取得最大值
取得最大值 . 13分
. 13分
练习册系列答案
相关题目
 ,
, .
.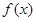 的最小正周期;
的最小正周期; 、
、 ,
, ,
, ,求
,求 的值.
的值.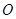 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径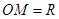 ,
, ,
, 与
与 之间的夹角为
之间的夹角为 .
.
 的面积
的面积 表示成
表示成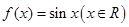 与
与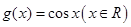 .
.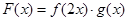 ,有下列结论:①
,有下列结论:①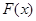 是奇函数;②
是奇函数;②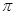 ;③
;③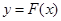 的图象关于点
的图象关于点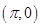 对称;④
对称;④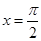 对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)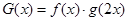 ,求满足
,求满足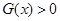 的
的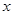 的取值范围;
的取值范围;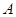 ,函数
,函数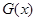 的值域为
的值域为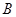 ,试判断集合
,试判断集合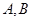 之间的关系.
之间的关系.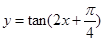 的图象的对称中心是()
的图象的对称中心是()



 上满足
上满足 的
的 的值有 个.
的值有 个.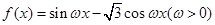 的图象与
的图象与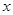 轴的两个相邻交点的距离等于
轴的两个相邻交点的距离等于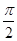 ,若将函数
,若将函数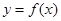 的图象向左平移
的图象向左平移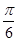 个单位得到函数
个单位得到函数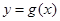 的图象,则
的图象,则



 -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为
sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为 .
. ]上的最大值和最小值.
]上的最大值和最小值.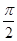 )的部分图象如图所示,则( )
)的部分图象如图所示,则( )
