题目内容
椭圆2x2+3y2=12的两焦点之间的距离为（ ）A．2
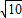
B．
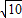
C．2
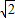
D．
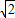
【答案】分析：把椭圆方程化为标准形式，求出a，b然后求出焦距即可．
解答：解：椭圆2x2+3y2=12化为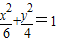
，所以a2=6；b2=4，所以c2=2，所以2c=
．
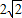椭圆2x2+3y2=12的两焦点之间的距离为：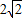
．
故选C．
点评：本题是基础题，考查椭圆的基本性质，注意a，b，c，的换算关系即可．
解答：解：椭圆2x2+3y2=12化为
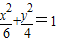，所以a2=6；b2=4，所以c2=2，所以2c=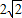．椭圆2x2+3y2=12的两焦点之间的距离为：
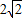．故选C．
点评：本题是基础题，考查椭圆的基本性质，注意a，b，c，的换算关系即可．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
椭圆2x2+3y2=12的两焦点之间的距离为（ ）
A、2
| ||
B、
| ||
C、2
| ||
D、
|