题目内容
(文科做)椭圆2x2+3y2=1的焦点坐标( )
分析:先把椭圆方程化为标准方程,再确定其几何量,从而求出椭圆的焦点坐标.
解答:解:椭圆方程化为标准方程为:
+
=1
∵
>
∴椭圆的焦点在x轴上,且a2=
,b2=
∴c2=a2-b2=
-
=
∴c=
故椭圆2x2+3y2=1的焦点坐标为(±
,0)
故选D.
| x2 | ||
|
| y2 | ||
|
∵
| 1 |
| 2 |
| 1 |
| 3 |
∴椭圆的焦点在x轴上,且a2=
| 1 |
| 2 |
| 1 |
| 3 |
∴c2=a2-b2=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
∴c=
| ||
| 6 |
故椭圆2x2+3y2=1的焦点坐标为(±
| ||
| 6 |
故选D.
点评:本题以椭圆方程为载体,考查椭圆的几何性质,解题的关键是把椭圆方程化为标准方程.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
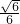 )
) )
) ,0)
,0)