Question

【题目】如图所示，三棱锥V﹣ABC中，VA=VB=AC=BC=2，AB=2 ，VC=1，线段AB的中点为D．

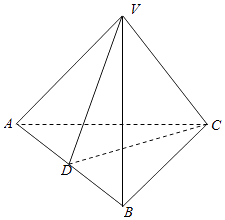
（1）求证：平面VCD⊥平面ABC；
（2）求三棱锥V﹣ABC的体积．

Answer 1

【答案】
（1）证明：如图所示：

∵VA=VB=2，AB=2 ，D为AB的中点，

∴VD⊥AB，VD= =1．

同理CD⊥AB，CD=1，CD∩VD=D，∴AB⊥平面VCD．

又∵AB平面ABC，∴平面VCD⊥平面ABC．

（2）解：∵AB⊥平面VCD，

∴三棱锥V﹣ABC的体积等于三棱锥A﹣VCD与B﹣VCD的体积之和．

∵VC=VD=CD=1，

∴△VCD的面积为：

= = ，

∴三棱锥V﹣ABC的体积为：

VV﹣ABC= = = ．

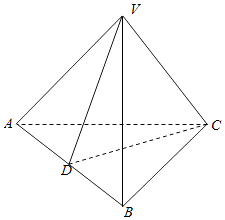
【解析】1、由已知条件可得VD⊥AB且VD=1，同理可得CD=1由线面垂直的判定定理可得AB⊥平面VCD再由面面垂直的判定定理可得平面VCD⊥平面ABC。
2、由题意可得三棱锥V﹣ABC的体积等于三棱锥A﹣VCD与B﹣VCD的体积之和所以VV﹣ABC= × S × A B。
【考点精析】通过灵活运用平面与平面垂直的判定，掌握一个平面过另一个平面的垂线，则这两个平面垂直即可以解答此题．