题目内容
1.已知函数$f(x)=\left\{{\begin{array}{l}{x(x+1),x≥0}\\{x(1-x),x<0}\end{array}}\right.$,则满足f(t-1)<f(2t)的实数t的取值范围是t>-1.分析 画出函数$f(x)=\left\{{\begin{array}{l}{x(x+1),x≥0}\\{x(1-x),x<0}\end{array}}\right.$的图象,分析函数的单调性,结合f(t-1)<f(2t),可得实数t的取值范围.
解答 解:函数$f(x)=\left\{{\begin{array}{l}{x(x+1),x≥0}\\{x(1-x),x<0}\end{array}}\right.$的图象如下图所示: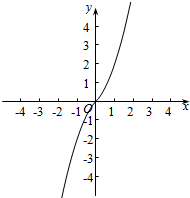
由图可得:函数f(x)在定义域R上为增函数,
若f(t-1)<f(2t),则t-1<2t,
解得:t>-1,
故答案为:t>-1
点评 本题考查的知识点是分段函数的应用,函数单调性的性质,难度不大,属于基础题.

练习册系列答案
相关题目
11.在数列11,111,1111,…中( )
| A. | 有完全平方数 | B. | 没有完全平方数 | C. | 没有偶数 | D. | 没有3的倍数 |
12.根据统计,一名工人组装第x件产品所用的时间(单位:分钟)为f(x)=$\left\{\begin{array}{l}\frac{c}{{\sqrt{x}}},x<a\\ \frac{c}{{\sqrt{a}}},x≥a\end{array}$(a,c为常数).已知工人组装第4件产品用时30分钟,组装第a件产品用时5分钟,那么c和a的值分别是( )
| A. | 75,25 | B. | 75,16 | C. | 60,144 | D. | 60,16 |
13.将函数y=cosx的图象上的每个点的横坐标变为原来的2倍、纵坐标不变,再将所得图象向右平移$\frac{π}{3}$个单位,则最后得到的图象对应的函数解析式为( )
| A. | $y=cos(2x-\frac{π}{3})$ | B. | $y=cos(2x-\frac{2π}{3})$ | C. | $y=cos(\frac{x}{2}-\frac{π}{3})$ | D. | $y=cos(\frac{x}{2}-\frac{π}{6})$ |