题目内容
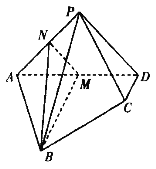
【题目】某校要在一条水泥路边安装路灯，其中灯杆的设计如图所示，AB为地面，CD，CE为路灯灯杆，CD⊥AB，∠DCE=
，在E处安装路灯，且路灯的照明张角∠MEN=
.已知CD=4m，CE=2m.
(1)当M，D重合时，求路灯在路面的照明宽度MN；
(2)求此路灯在路面上的照明宽度MN的最小值.
【答案】(1) 
；(2) 
.
【解析】
（1）用余弦定理求出
，进而求出
，结合已知条件，求出
，用正弦定理求出
；
（2）由面积公式，余弦定理结合基本不等式，即可求出结果.
(1)当M，D重合时，
由余弦定理知，
∴
∵
∴
，
∵
∴
∵
∴在ΔEMN中，由正弦定理可知，
解得
；
(2)易知E到地面的距离
=5m
由三角形面积公式可知，
∴
，又由余弦定理可知，
，
当且仅当EM=EN时，等号成立，
∴
，解得
答:(1)路灯在路面的照明宽度为
m；
(2)照明宽度MV的最小值为.
练习册系列答案
53随堂测系列答案
相关题目
