题目内容
7.已知甲、乙两煤矿每年的产量分别为200万吨和260万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站毎年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/t和1.5元/t,乙煤矿运往东车站和西车站的运费价格分别为0.8元/t和1.6元/t.煤矿应怎样编制调运方案,能使总运费最少?分析 设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,那么总运费:z=x+1.5(200-x)+0.8y+1.6(260-y),即z=716-0.5x-0.8y.由题意得到关于x,y的不等式组,由线性规划知识求得能使总运费最少的x,y值.
解答 解:设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,那么总运费:
z=x+1.5(200-x)+0.8y+1.6(260-y)(万元),
即z=716-0.5x-0.8y.
x、y应满足$\left\{\begin{array}{l}{0≤x≤200}\\{0≤y≤260}\\{x+y≤280}\\{200-x+260-y≤360}\end{array}\right.$,
作出上面的不等式组所表示的平面区域,如图.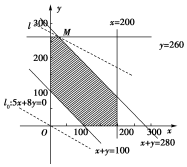 .
.
设直线x+y=280与y=260的交点为M,则M(20,260).
把直线l0:5x+8y=0向上平移至经过平面区域上的点M时,z的值最小.
∵点M的坐标为(20,260),
∴甲煤矿生产的煤向东车站运20万吨,向西车站运180万吨,乙煤矿生产的煤全部运往东车站时,总运费最少.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
12.方程x2+y2cosα=1(α∈R)不能表示的曲线为( )
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 圆 |
19.设Sn为等比数列{an}的前n项和,且8a2+a5=0,则S3:S2的值为( )
| A. | -3 | B. | 5 | C. | -8 | D. | -11 |
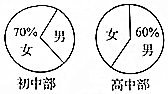 某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为137.
某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为137.