题目内容
1.已知F1,F2分别是双曲线3x2-y2=3a2(a>0)的左,右焦点,P是抛物线y2=8ax与双曲线的一个交点,若|PF1|+|PF2|=12,则抛物线的准线方程为x=-2.分析 设P(m,n),且P在第一象限,求得双曲线的a,b,c,运用双曲线的定义可得|PF2|=6-a,求得抛物线的焦点和准线方程,运用抛物线的定义,可得m=6-3a,求得n,代入双曲线的方程,解方程可得a=1,进而得到准线方程.
解答 解:设P(m,n),且P在第一象限,
双曲线3x2-y2=3a2(a>0)即为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3{a}^{2}}$=1,
可得b=$\sqrt{3}$a,c=$\sqrt{{a}^{2}+{b}^{2}}$=2a,
由双曲线的定义可得|PF1|-|PF2|=2a,
又|PF1|+|PF2|=12,可得
|PF2|=6-a,
由抛物线y2=8ax可得焦点为(2a,0),准线方程为x=-2a,
由抛物线的定义可得6-a=m+2a,
解得m=6-3a,n2=8a(6-3a),
代入双曲线的方程可得
$\frac{(6-3a)^{2}}{{a}^{2}}$-$\frac{8a(6-3a)}{3{a}^{2}}$=1,
解得a=1或$\frac{9}{4}$(舍去),
则准线的方程为x=-2.
故答案为:x=-2.
点评 本题考查双曲线和抛物线的定义、方程和性质,考查点满足曲线方程,以及化简整理的运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.在(2x-y)7的展开式中各项的系数之和为( )
| A. | 1 | B. | -1 | C. | 128 | D. | -128 |
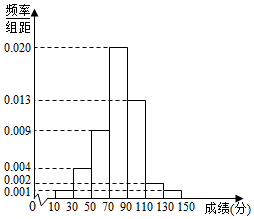 襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.
襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.