题目内容
已知数列{an},Sn是其n前项的和,且满足3an=2Sn+n(n∈N*)
(1)求证:数列{an+
}为等比数列;
(2)记Tn=S1+S2+L+Sn,求Tn的表达式;
(3)记Cn=
(an+
),求数列{nCn}的前n项和Pn.
(1)求证:数列{an+
| 1 |
| 2 |
(2)记Tn=S1+S2+L+Sn,求Tn的表达式;
(3)记Cn=
| 2 |
| 3 |
| 1 |
| 2 |
分析:(1)由3an=2Sn+n知,当n≥2时,3an-1=2Sn-1+n-1,作差后可知an=3an-1+1,于是易证数列{an+
}是首项为
,公比为3的为等比数列;
(2)由(1)知an=
×3n-
,利用分组求和法即可求得Tn的表达式;
(3)由(2)易知Cn=3n-1,利用错位相减法即可求得数列{nCn}的前n项和Pn.
| 1 |
| 2 |
| 3 |
| 2 |
(2)由(1)知an=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由(2)易知Cn=3n-1,利用错位相减法即可求得数列{nCn}的前n项和Pn.
解答:解:(1)∵3an=2Sn+n,
∴a1=1,
当n≥2时,3(an-an-1)=2an+1,即an=3an-1+1,
∴an+
=3an-1+1+
=3(an-1+
),
∴数列{an+
}是首项为
,公比为3的为等比数列;
(2)由(1)知,an+
=
•3n-1,
∴an=
×3n-
,
∴Sn=a1+a2+…+an
=
•
-
=
•3n-
(2n+3),
∴Tn=S1+S2+…+Sn
=
(3+32+…+3n)-
×
=
•
-
=
(3n-1)-
.
(3)∵Cn=
(an+
)=
×
×3n=3n-1,
∴Pn=1×30+2×3+3×32+…+n•3n-1,
∴3Pn=1×3+2×32+…+(n-1)•3n-1+n•3n,
两式相减得:
-2Pn=1+3+32+…+3n-1-n•3n
=
-n•3n
=
×3n-
,
∴Pn=
.
∴a1=1,
当n≥2时,3(an-an-1)=2an+1,即an=3an-1+1,
∴an+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴数列{an+
| 1 |
| 2 |
| 3 |
| 2 |
(2)由(1)知,an+
| 1 |
| 2 |
| 3 |
| 2 |
∴an=
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=a1+a2+…+an
=
| 1 |
| 2 |
| 3(1-3n) |
| 1-3 |
| n |
| 2 |
=
| 3 |
| 4 |
| 1 |
| 4 |
∴Tn=S1+S2+…+Sn
=
| 3 |
| 4 |
| 1 |
| 4 |
| (5+2n+3)n |
| 2 |
=
| 3 |
| 4 |
| 3(1-3n) |
| 1-3 |
| n(n+4) |
| 4 |
=
| 9 |
| 8 |
| n(n+4) |
| 4 |
(3)∵Cn=
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
∴Pn=1×30+2×3+3×32+…+n•3n-1,
∴3Pn=1×3+2×32+…+(n-1)•3n-1+n•3n,
两式相减得:
-2Pn=1+3+32+…+3n-1-n•3n
=
| 1-3n |
| 1-3 |
=
| 1-2n |
| 2 |
| 1 |
| 2 |
∴Pn=
| 1+(2n-1)•3n |
| 4 |
点评:本题考查数列的求和,着重考查等比关系的确定,突出考查等比数列的求和公式与错位相减法、分组求和法的综合应用,属于难题.

练习册系列答案
相关题目
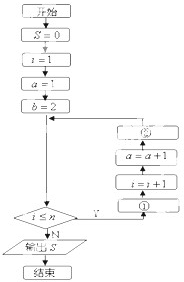 已知数列{an}的通项公式为an=n•2n,为了求数列{an}的和,现已给出该问题的算法程序框图.
已知数列{an}的通项公式为an=n•2n,为了求数列{an}的和,现已给出该问题的算法程序框图.