题目内容

方程f（x）=0的根称为函数f（x）的零点，定义在上的函数f（x），其导函数f′（x）的图象如图所示，且f（x1）•f（x2）＜0，则函数f（x）的零点个数是（ ）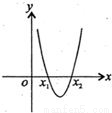

A．i1
B．.2
C．.3
D．.1或3
【答案】分析：根据导函数f′（x）的图象可知x1与x2为导数为零两个根，从而函数f（x）有两个极值点，再根据f（x1）•f（x2）＜0，则两极值点分布在x轴两侧，从而得到函数f（x）的零点个数．
解答：解：根据导函数f′（x）的图象可知x1与x2为导数为零两个根
∴函数f（x）有两个极值点
而f（x1）•f（x2）＜0，则两极值点分布在x轴两侧
故函数f（x）的零点个数是3
故选：C
点评：本题主要考查了函数的零点，以及导函数与原函数之间的关系，同时考查了数形结合的思想，属于基础题．
练习册系列答案
相关题目
9、方程f（x）=0的根称为函数f（x）的零点，定义在上的函数f（x），其导函数f′（x）的图象如图所示，且f（x1）•f（x2）＜0，则函数f（x）的零点个数是（　　）
若函数f（x）=ax3+bx2+cx+d（a≠0），[f′（α）]2+[f′（β）]2=0，f（α）+f（β）=0（其中α，β∈R且α≠β），则下列选项中一定是方程f（x）=0的根的是（　　）
设函数f（x）=x3-2x2-4x-7
（Ⅰ）求f（x）的单调区间及极小值；
（Ⅱ）确定方程f（x）=0的根的一个近似值，使其误差不超过0.5，并说明理由；
（Ⅲ）当a＞2时，证明：对任意的实数x＞2，恒有f（x）≥f（a）+f′（a）（x-a）．
已知函数f（x）是定义在R上的偶函数，且在（0，+∞）上是减函数，若f(
1
3
)＞0＞f(
2
)，则方程f（x）=0的根的个数是（　　）
A、2B、2或1C、3D、2或3
方程f（x）=0的根称为函数f（x）的零点，定义R+在上的函数f（x），其导函数f′（x）的图象如图所示，且f（x1）f（x2）＜0，则函数f（x）的零点个数是
3
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网