题目内容
 观察右列等式:
观察右列等式:可以推测当n∈N*时,有:13+23+…+n3=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据已知中,13=12;13+23=(1+2)2;13+23+33=(1+2+3)2;13+23+33+43=(1+2+3+4)2;13+23+33+43+53=(1+2+3+4+5)2;…我们分析左边式子中的数与右边式了中的数之间的关系,归纳分析后,即可得到答案.
解答:解:由已知中的等式
13=12;
13+23=(1+2)2;
13+23+33=(1+2+3)2;
13+23+33+43=(1+2+3+4)2;
13+23+33+43+53=(1+2+3+4+5)2;
…
13+23+33+…+n3═(1+2+…+5)2;
即 13+23+33++n3=(
)2=
,
故答案为:
.
13=12;
13+23=(1+2)2;
13+23+33=(1+2+3)2;
13+23+33+43=(1+2+3+4)2;
13+23+33+43+53=(1+2+3+4+5)2;
…
13+23+33+…+n3═(1+2+…+5)2;
即 13+23+33++n3=(
| n(n+1) |
| 2 |
| n2(n+1)2 |
| 4 |
故答案为:
| n2(n+1)2 |
| 4 |
点评:本题考查的知识点是归纳推理其中分析已知中的式子,分析出两个式子之间的数据变化规律是解答的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
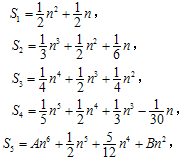 记
记 观察右列等式:
观察右列等式:



 ,当k=1,2,3…时,观察如图等式:可以推测,A-B= .
,当k=1,2,3…时,观察如图等式:可以推测,A-B= .




