题目内容
16.在正三棱柱ABC-A1B1C1中,若AB=$\sqrt{2}$BB1,则AB1与BC1所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{2}$ |
分析 利用向量加法的三角形法则,可将AB1与C1B的方向向量分别用三棱柱的棱对应的向量表示,进而设BB1=1,AB=$\sqrt{2}$,分析出两向量数量积为0,进而得到两直线互相垂直.
解答 解: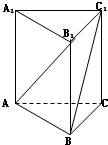 ∵AB=$\sqrt{2}$BB1,设BB1=1,AB=$\sqrt{2}$,
∵AB=$\sqrt{2}$BB1,设BB1=1,AB=$\sqrt{2}$,
∴$\overrightarrow{{AB}_{1}}$•$\overrightarrow{{BC}_{1}}$=($\overrightarrow{AB}$+$\overrightarrow{{BB}_{1}}$ )•($\overrightarrow{BC}$+$\overrightarrow{{CC}_{1}}$ )
=$\overrightarrow{AB}$•$\overrightarrow{{CC}_{1}}$+$\overrightarrow{AB}$•$\overrightarrow{BC}$-$\overrightarrow{{BB}_{1}}$2+$\overrightarrow{{BB}_{1}}$•$\overrightarrow{BC}$
=0+$\sqrt{2}$×$\sqrt{2}$×cos$\frac{π}{3}$-1+0=0
∴直线AB1与BC1所成角为$\frac{π}{2}$,
故选:D.
点评 本题考查的知识点是异面直线及其所成的角,其中利用向量法将空间直线夹角转化为向量夹角是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.等差数列{an}的前n项和为Sn,若a1000+a1018=2,则S2017=( )
| A. | 1008 | B. | 1009 | C. | 2016 | D. | 2017 |
5.在面积为S的△ABC的边AB含任取一点P,则△PBC的面积大于$\frac{S}{4}$的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |