题目内容
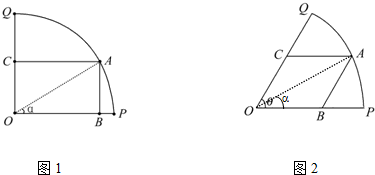 如图1所示,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.记∠AOP=α.
如图1所示,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.记∠AOP=α.
(1)若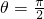 ,如图1,当角α取何值时,能使矩形ABOC的面积最大;
,如图1,当角α取何值时,能使矩形ABOC的面积最大;
(2)若 ,如图2,当角α取何值时,能使平行四边形ABOC的面积最大.并求出最大面积.
,如图2,当角α取何值时,能使平行四边形ABOC的面积最大.并求出最大面积.
解:(1)若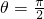 ,由题意可得 AB=sinα,BO=cosα,故矩形ABOC的面积S=AB•BO=
,由题意可得 AB=sinα,BO=cosα,故矩形ABOC的面积S=AB•BO= sin2α,
sin2α,
故当α= 时,能使矩形ABOC的面积最大.
时,能使矩形ABOC的面积最大.
(2)若 ,由题意可得0<α<
,由题意可得0<α< ,作AH⊥OP,H为垂足,则AH=sinα,OH=cosα,tan∠ABH=
,作AH⊥OP,H为垂足,则AH=sinα,OH=cosα,tan∠ABH=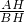 =tan
=tan =
= ,
,
故BH= sinα,∴OB=cosα-
sinα,∴OB=cosα- sinα.
sinα.
故平行四边形ABOC的面积S′=OB•AH=(cosα- sinα )sinα=sinαcosα-
sinα )sinα=sinαcosα- sin2α
sin2α
= sin2α-
sin2α- ×
×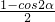 =
= sin2α-
sin2α- cos2α-
cos2α- =
= sin(2α+
sin(2α+ )-
)- .
.
由于0<α< ,故
,故 <2α+
<2α+ <
< ,故当 2α+
,故当 2α+ =
= 时,S′取得最大值为
时,S′取得最大值为  .
.
分析:(1)若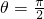 ,由题意可得 AB=sinα,BO=cosα,求得矩形ABOC的面积S=AB•BO=
,由题意可得 AB=sinα,BO=cosα,求得矩形ABOC的面积S=AB•BO= sin2α,由此求得角α取何值时,能使矩形ABOC的面积最大.
sin2α,由此求得角α取何值时,能使矩形ABOC的面积最大.
(2)若 ,作AH⊥OP,H为垂足,则AH=sinα,OH=cosα,BH=
,作AH⊥OP,H为垂足,则AH=sinα,OH=cosα,BH= sinα,可得OB=cosα-
sinα,可得OB=cosα- sinα.化简平行四边形ABOC的面积S′=OB•AH,等于
sinα.化简平行四边形ABOC的面积S′=OB•AH,等于  sin(2α+
sin(2α+ )-
)- .由0<α<
.由0<α< ,可得当 2α+
,可得当 2α+ =
= 时,S′取得最大值为
时,S′取得最大值为  .
.
点评:本题主要考查两角和差的正弦、余弦公式的应用,二倍角公式,正弦函数的定义域和值域,属于中档题.
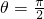 ,由题意可得 AB=sinα,BO=cosα,故矩形ABOC的面积S=AB•BO=
,由题意可得 AB=sinα,BO=cosα,故矩形ABOC的面积S=AB•BO= sin2α,
sin2α,故当α=
 时,能使矩形ABOC的面积最大.
时,能使矩形ABOC的面积最大.(2)若
 ,由题意可得0<α<
,由题意可得0<α< ,作AH⊥OP,H为垂足,则AH=sinα,OH=cosα,tan∠ABH=
,作AH⊥OP,H为垂足,则AH=sinα,OH=cosα,tan∠ABH=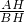 =tan
=tan =
= ,
,故BH=
 sinα,∴OB=cosα-
sinα,∴OB=cosα- sinα.
sinα.故平行四边形ABOC的面积S′=OB•AH=(cosα-
 sinα )sinα=sinαcosα-
sinα )sinα=sinαcosα- sin2α
sin2α =
 sin2α-
sin2α- ×
×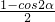 =
= sin2α-
sin2α- cos2α-
cos2α- =
= sin(2α+
sin(2α+ )-
)- .
.由于0<α<
 ,故
,故 <2α+
<2α+ <
< ,故当 2α+
,故当 2α+ =
= 时,S′取得最大值为
时,S′取得最大值为  .
.分析:(1)若
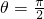 ,由题意可得 AB=sinα,BO=cosα,求得矩形ABOC的面积S=AB•BO=
,由题意可得 AB=sinα,BO=cosα,求得矩形ABOC的面积S=AB•BO= sin2α,由此求得角α取何值时,能使矩形ABOC的面积最大.
sin2α,由此求得角α取何值时,能使矩形ABOC的面积最大.(2)若
 ,作AH⊥OP,H为垂足,则AH=sinα,OH=cosα,BH=
,作AH⊥OP,H为垂足,则AH=sinα,OH=cosα,BH= sinα,可得OB=cosα-
sinα,可得OB=cosα- sinα.化简平行四边形ABOC的面积S′=OB•AH,等于
sinα.化简平行四边形ABOC的面积S′=OB•AH,等于  sin(2α+
sin(2α+ )-
)- .由0<α<
.由0<α< ,可得当 2α+
,可得当 2α+ =
= 时,S′取得最大值为
时,S′取得最大值为  .
.点评:本题主要考查两角和差的正弦、余弦公式的应用,二倍角公式,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
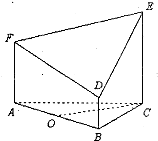 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.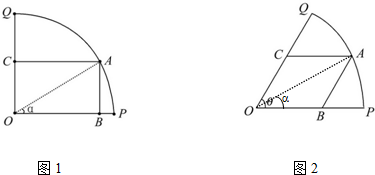 如图1所示,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.记∠AOP=α.
如图1所示,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.记∠AOP=α. 如图所示,已知点G是△ABO的重心.
如图所示,已知点G是△ABO的重心.