题目内容
已知数列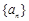 的前
的前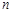 项和为
项和为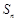 满足
满足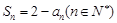 .
.
(Ⅰ)函数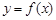 与函数
与函数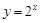 互为反函数,令
互为反函数,令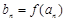 ,求数列
,求数列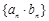 的前
的前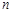 项和
项和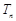 ;
;
(Ⅱ)已知数列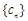 满足
满足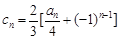 ,证明:对任意的整数
,证明:对任意的整数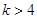 ,有
,有 .
.
(Ⅰ) ;(Ⅱ)详见解析;
;(Ⅱ)详见解析;
解析试题分析:(Ⅰ)由于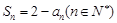 ,可知数列
,可知数列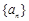 是以2为首项,2为公比的等比数列,所以
是以2为首项,2为公比的等比数列,所以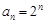 ;又函数
;又函数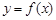 与函数
与函数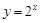 互为反函数,知
互为反函数,知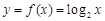 ,可求
,可求 ,在利用错位相减求数列
,在利用错位相减求数列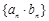 的前
的前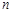 项和
项和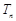 ;(Ⅱ)结合(Ⅰ)和
;(Ⅱ)结合(Ⅰ)和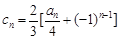 ,求出
,求出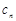 通项公式,在求出
通项公式,在求出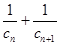 ,利用不等式放缩求出
,利用不等式放缩求出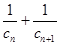
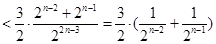 ,对k按当
,对k按当 且
且 为偶数和当
为偶数和当 且
且 为奇数分类讨论利用等比数列前n项和公式求和/
为奇数分类讨论利用等比数列前n项和公式求和/
试题解析:(Ⅰ)由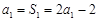 ,得
,得
当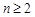 时,有
时,有 ,
,
所以数列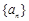 是以2为首项,2为公比的等比数列,所以
是以2为首项,2为公比的等比数列,所以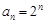
由题意得 ,所以
,所以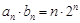
 ①
① 得
得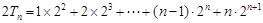 ②
②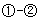 得
得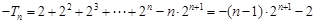 ,所以
,所以
(Ⅱ)由通项公式得 ,当
,当 且
且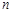 为奇数时
为奇数时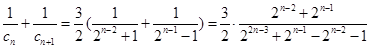
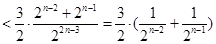
①当 且
且 为偶数时
为偶数时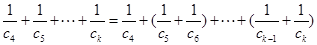
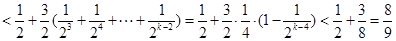
②当 且
且 为奇数时
为奇数时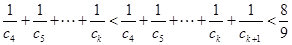 .
.
考点:1.数列的地推关系;2.错位相减法求和;3.不等式放缩在数列中的应用.

练习册系列答案
相关题目
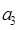 成等差数列.
成等差数列.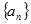 是公差不为零的等差数列,
是公差不为零的等差数列,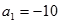 ,且
,且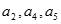 成等比数列.
成等比数列.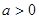 ,求数列
,求数列 的前n项和
的前n项和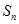 .
.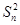 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.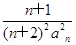 ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn< 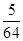 .
.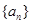 的首项
的首项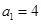 ,公差
,公差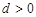 ,且
,且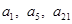 分别是正数等比数列
分别是正数等比数列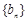 的
的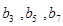 项.
项.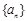 与
与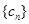 对任意
对任意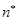 均有
均有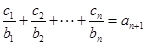 成立,设
成立,设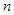 项和为
项和为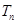 ,求
,求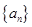 的前
的前 项和为
项和为 ,且
,且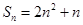 ,
, ,数列
,数列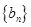 满足
满足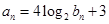 ,
,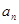 ,
,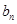 ;
;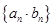 的前
的前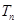 .
.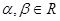 且
且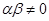 ,数列
,数列 满足
满足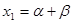 ,
,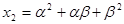 ,
,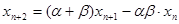 (
(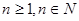 ),令
),令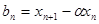 ,
,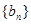 是等比数列;
是等比数列;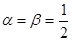 ,求
,求 项和
项和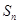 .
.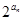 }的前n项和Sn.
}的前n项和Sn.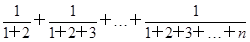 .
.