题目内容
(本小题12分)
已知函数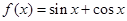 ,
,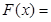
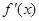

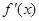
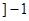 ,
,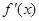 是
是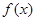 的导函数.
的导函数.
(I)若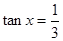 ,求
,求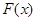 的值;(Ⅱ)求
的值;(Ⅱ)求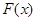 的单调减区间.
的单调减区间.
【答案】
(1) . (2)
. (2) 的单调减区间为
的单调减区间为
 。
。
【解析】本试题主要是考查了导数在研究函数中的运用,求解函数的单调区间,以及三角函数的化简求值的综合运用。
(1)根据已知条件,函数 ,
,



 ,
, 是
是 的导函数.那么可知
的导函数.那么可知 ,
, 化简得到结论。
化简得到结论。
(2)由(1)知:
 ,借助于三角函数的单调区间得到所求的区间。
,借助于三角函数的单调区间得到所求的区间。
解:(1)∵
∴

= 

= .
…………6分
.
…………6分
(2)由(1)知:
 .
.
令 得:
得:
∴ 的单调减区间为
的单调减区间为  …………12分
…………12分

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
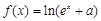 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数. 在
在 及
及 所在的取值范围上恒成立,求
所在的取值范围上恒成立,求 的取值范围;
的取值范围; 的方程
的方程 的根的个数.
的根的个数. 满足
满足 且
且 .
. 时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.
的范围.
 ,求
,求 的最大值;
的最大值;  ,离心率为
,离心率为 ,且过点
,且过点 ,
,
 (其中
(其中 为参数)所过的定点
为参数)所过的定点 恰在双曲线上,求证:
恰在双曲线上,求证: 。
。 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。 直线
直线 ,且直线
,且直线 与曲线
与曲线 相切于点
相切于点 ,求直线
,求直线 的坐标。
的坐标。