题目内容

设（1+x）+（1+x）2+（1+x）3+…+（1+x）n=a0+a1x+a2x2+…+anxn，当a0+a1+a2+…+an=254时，n等于（　　）
分析：观察已知条件a0+a1+a2+…+an=254，可令（1+x）+（1+x）2+（1+x）3+…+（1+x）n=a0+a1x+a2x2+…+anxn中的x=1，可得254=2n+1-2，解之即可．
解答：解：∵（1+x）+（1+x）2+（1+x）3+…+（1+x）n=a0+a1x+a2x2+…+anxn
∴令x=1得2+22+23+…+2n=a0+a1+a2+…+an，
而a0+a1+a2+…+an=254=
2(1-2n)
1-2
=2n+1-2，
∴n=7
故答案为：C
点评：本题主要考查了二项式系数的性质，以及赋值法的应用，属于基础题．
练习册系列答案
相关题目
设f（x）是定义在R上的奇函数，且f（1）=0，当x＞0时，有f（x）＞xf′（x）恒成立，则不等式xf（x）＞0的解集为（　　）
设f（x）是定义在R上的偶函数，且f（2+x）=f（2-x），当x∈[-2，0）时，f（x）=(
2
2
)x-1，若在区间（-2，6）内的关于x的方程f（x）-logga（x+2）=0（a＞0且a≠1）恰有4个不同的实数根，则实数a的取值范围是（　　）
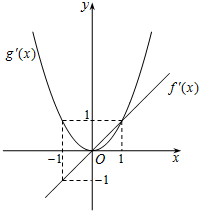（2013•武汉模拟）已知函数f'（x）、g'（x）分别是二次函数f（x）和三次函数g（x）的导函数，它们在同一坐标系下的图象如图所示：
①若f（1）=1，则f（-1）=
1
1
；
②设函数h（x）=f（x）-g（x），则h（-1），h（0），h（1）的大小关系为
h（0）＜h（1）＜h（-1）
h（0）＜h（1）＜h（-1）
．（用“＜”连接）
（2012•韶关二模）定义符号函数sgnx=
1，x＞0
0，x=0
-1，x＜0
，设f（x）=
sgn(
1
2
-x)+1
2
•f1(x)+
sgn(x-
1
2
)+1
2
•f2（x），x∈[0，1]，其中f1（x）=x+
1
2
，f2（x）=2（1-x），若f[f(a)]∈[0，
1
2
)，则实数a的取值范围是（　　）
设f（x）=（x+1）n（其中n∈N+）．
（1）若f（x）=a0+a1（x-1）+a2（x-1）2+a3（x-1）3+…+an（x-1）n，求a0及Sn=a1+a2+a3+…+an；
（2）当n=2013，计算：
C
1
2013
-2
C
2
2013
+…+k
C
k
2013
（-1）k-1+…+2013
C
2013
2013
（-1）2012．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网