Question

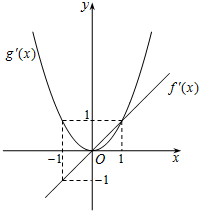（2013•武汉模拟）已知函数f'（x）、g'（x）分别是二次函数f（x）和三次函数g（x）的导函数，它们在同一坐标系下的图象如图所示：
①若f（1）=1，则f（-1）=

1

；
②设函数h（x）=f（x）-g（x），则h（-1），h（0），h（1）的大小关系为

h（0）＜h（1）＜h（-1）

．（用“＜”连接）

Answer 1

分析：①先结合函数图形求出f'（x）与g'（x）的解析式，然后求出原函数，根据f（1）=1，可求出f（-1）的值；
②求出函数h（x）=f（x）-g（x）的解析式，然后将-1，0，1代入比较即可求出h（-1），h（0），h（1）的大小关系．

解答：解：根据函数f'（x）、g'（x）分别是二次函数f（x）和三次函数g（x）的导函数
结合图象可知f'（x）=x、g'（x）=x²；
则f（x）=

1

2

x²+C，g（x）=

1

3

x³+C'，
①∵f（1）=1∴C=

1

2

则f（x）=

1

2

x²+

1

2

，
∴f（-1）=1
②h（x）=f（x）-g（x）=

1

2

x²-

1

3

x³+C-C'
记C-C'=m为常数
则h（-1）=

5

6

+m，h（0）=m，h（1）=

1

6

+m
∴h（0）＜h（1）＜h（-1）
故答案为：1，h（0）＜h（1）＜h（-1）

点评：本题主要考查了利用图形求解析式，以及根据导函数求原函数等知识，同时考查了比较函数值大小，属于中档题．