题目内容
△OAB中, =(5cosα,5sinα),
=(5cosα,5sinα), =(2cosβ,2sinβ),S△AOB=
=(2cosβ,2sinβ),S△AOB= ,则
,则 •
• =________.
=________.
±5
分析:由题意可得: ,
,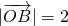 ,由三角形的面积公式可得:sin
,由三角形的面积公式可得:sin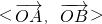 =
= ,即可得到cos
,即可得到cos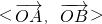 =±
=± ,进而结合平面向量的数量积公式求出
,进而结合平面向量的数量积公式求出 的数值.
的数值.
解答:由题意可得: =(5cosα,5sinα),
=(5cosα,5sinα), =(2cosβ,2sinβ),
=(2cosβ,2sinβ),
∴ ,
,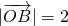 ,
,
∵S△AOB= ,即S△AOB=
,即S△AOB= =
= ,
,
∴sin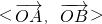 =
= ,
,
∵ ,
,
∴cos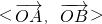 =±
=± ,
,
所以 =
= =±5.
=±5.
故答案为:±5.
点评:本题主要考查三角形的面积公式与平面向量的数量积公式,以及考查两角差的余弦公式的逆用与特殊角的三角函数值,此题属于基础题,综合性交强,考查学生的运算能力与分析问题解决问题的能力.
分析:由题意可得:
 ,
,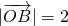 ,由三角形的面积公式可得:sin
,由三角形的面积公式可得:sin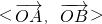 =
= ,即可得到cos
,即可得到cos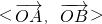 =±
=± ,进而结合平面向量的数量积公式求出
,进而结合平面向量的数量积公式求出 的数值.
的数值.解答:由题意可得:
 =(5cosα,5sinα),
=(5cosα,5sinα), =(2cosβ,2sinβ),
=(2cosβ,2sinβ),∴
 ,
,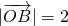 ,
,∵S△AOB=
 ,即S△AOB=
,即S△AOB= =
= ,
,∴sin
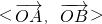 =
= ,
,∵
 ,
,∴cos
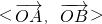 =±
=± ,
,所以
 =
= =±5.
=±5.故答案为:±5.
点评:本题主要考查三角形的面积公式与平面向量的数量积公式,以及考查两角差的余弦公式的逆用与特殊角的三角函数值,此题属于基础题,综合性交强,考查学生的运算能力与分析问题解决问题的能力.

练习册系列答案
相关题目