题目内容
【题目】设F是椭圆C：
（a＞b＞0）的一个焦点，P是椭圆C上的点，圆x2＋y2＝
与线段PF交于A，B两点，若A，B三等分线段PF，则椭圆C的离心率为（ ）
A.
B.
C.
D.
【答案】D
【解析】
取线段PF的中点H，连接OH，OA，由题意可得OH⊥AB，设|OH|＝d，根据椭圆的定义以及在Rt△OHA中，可得a＝5d，在Rt△OHF中，利用勾股定理即可求解.
如图，取线段PF的中点H，连接OH，OA.
设椭圆另一个焦点为E，连接PE.
∵A，B三等分线段PF，∴H也是线段AB的中点，即OH⊥AB.
设|OH|＝d，则|PE|＝2d，|PF|＝2a－2d，|AH|＝
.
在Rt△OHA中，|OA|2＝|OH|2＋|AH|2，解得a＝5d.
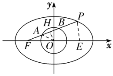
在Rt△OHF中，|FH|＝
，|OH|＝
，|OF|＝c.
由|OF|2＝|OH|2＋|FH|2，
化简得17a2＝25c2，
.
即椭圆C的离心率为
.
故选：D.
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
