题目内容
数列{bn}的首项b1=1,前n项和为Sn,点(n,Sn)、(4,10)都在二次函数y=ax2+bx的图象上,数列{an}满足 =2n.
=2n.
(Ⅰ)求证:数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)令cn=( )
) ,Rn=
,Rn=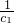 +
+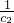 +
+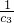 +…+
+…+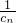 .
.
试比较Rn与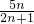 的大小,并证明你的结论.
的大小,并证明你的结论.
解:(Ⅰ)证明:∵b1=1,∴S1=1
∴点(1,1)、(4,10)都在二次函数y=ax2+bx的图象上
∴a+b=1,16a+4b=10,解得a= ,b=
,b= .
.
∴Sn= n2+
n2+ n.则n≥2时,Sn-1=
n.则n≥2时,Sn-1= (n-1)2+
(n-1)2+ (n-1).
(n-1).
∴bn=Sn-Sn-1= n2+
n2+ n-[
n-[ (n-1)2+
(n-1)2+ (n-1)]=n(n≥2).
(n-1)]=n(n≥2).
又b1=1也适合,所以bn=n(n∈N+).则bn-bn-1=1.
∴数列{bn}是首项为1,公差为1的等差数列.
又 =2n ∴an=
=2n ∴an=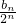 =
= .
.
(Ⅱ)证明:∵cn=( )
) =
= •
• =
= ∴
∴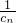 =
=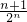
∴Rn=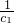 +
+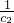 +
+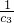 +…+
+…+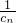 =
= +
+ +
+ +…+
+…+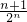 ①.
①.
∴ Rn=
Rn= ,②
,②
两式相减得 Rn=
Rn=
∴Rn=3- ,Rn-
,Rn-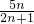 =
=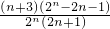 .
.
所以只需要比较2n与2n+1的大小即可.
当n=1时,2n<2n+1,所以Rn<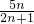 ,
,
当n=2时,2n<2n+1,所以Rn<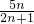 ,
,
当n≥3时,2n=(1+1)n=1+n++n+1>2n+1,所以Rn>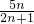 .(12分)
.(12分)
分析:(Ⅰ)先由b1=1得S1=1,再利用点(1,1)、(4,10)都在二次函数y=ax2+bx的图象上求出a= ,b=
,b= ;再利用根据bn和Sn的关系:bn=Sn-Sn-1 (n≥2)求解数列bn的通项公式即可证:数列{bn}是等差数列,再代入满足
;再利用根据bn和Sn的关系:bn=Sn-Sn-1 (n≥2)求解数列bn的通项公式即可证:数列{bn}是等差数列,再代入满足 =2n.即可求出求数列{an}的通项公式;
=2n.即可求出求数列{an}的通项公式;
(Ⅱ)先求出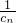 =
=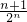 ,再对其用错位相减法求和,得到Rn=3-
,再对其用错位相减法求和,得到Rn=3- ,让Rn与
,让Rn与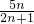 作差,整理后分类比较大小即可.
作差,整理后分类比较大小即可.
点评:本题考查了已知前n项和为Sn求数列{an}的通项公式,根据an和Sn的关系:an=Sn-Sn-1 (n≥2)求解数列的通项公式.另外,须注意公式成立的前提是n≥2,所以要验证n=1时通项是否成立,若成立则:an=Sn-Sn-1 (n≥1);若不成立,则通项公式为分段函数.
∴点(1,1)、(4,10)都在二次函数y=ax2+bx的图象上
∴a+b=1,16a+4b=10,解得a=
 ,b=
,b= .
.∴Sn=
 n2+
n2+ n.则n≥2时,Sn-1=
n.则n≥2时,Sn-1= (n-1)2+
(n-1)2+ (n-1).
(n-1).∴bn=Sn-Sn-1=
 n2+
n2+ n-[
n-[ (n-1)2+
(n-1)2+ (n-1)]=n(n≥2).
(n-1)]=n(n≥2).又b1=1也适合,所以bn=n(n∈N+).则bn-bn-1=1.
∴数列{bn}是首项为1,公差为1的等差数列.
又
 =2n ∴an=
=2n ∴an=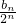 =
= .
.(Ⅱ)证明:∵cn=(
 )
) =
= •
• =
= ∴
∴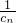 =
=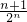
∴Rn=
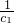 +
+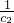 +
+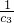 +…+
+…+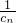 =
= +
+ +
+ +…+
+…+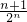 ①.
①.∴
 Rn=
Rn= ,②
,②两式相减得
 Rn=
Rn=
∴Rn=3-
 ,Rn-
,Rn-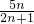 =
=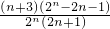 .
.所以只需要比较2n与2n+1的大小即可.
当n=1时,2n<2n+1,所以Rn<
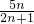 ,
,当n=2时,2n<2n+1,所以Rn<
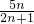 ,
,当n≥3时,2n=(1+1)n=1+n++n+1>2n+1,所以Rn>
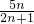 .(12分)
.(12分)分析:(Ⅰ)先由b1=1得S1=1,再利用点(1,1)、(4,10)都在二次函数y=ax2+bx的图象上求出a=
 ,b=
,b= ;再利用根据bn和Sn的关系:bn=Sn-Sn-1 (n≥2)求解数列bn的通项公式即可证:数列{bn}是等差数列,再代入满足
;再利用根据bn和Sn的关系:bn=Sn-Sn-1 (n≥2)求解数列bn的通项公式即可证:数列{bn}是等差数列,再代入满足 =2n.即可求出求数列{an}的通项公式;
=2n.即可求出求数列{an}的通项公式;(Ⅱ)先求出
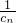 =
=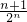 ,再对其用错位相减法求和,得到Rn=3-
,再对其用错位相减法求和,得到Rn=3- ,让Rn与
,让Rn与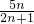 作差,整理后分类比较大小即可.
作差,整理后分类比较大小即可.点评:本题考查了已知前n项和为Sn求数列{an}的通项公式,根据an和Sn的关系:an=Sn-Sn-1 (n≥2)求解数列的通项公式.另外,须注意公式成立的前提是n≥2,所以要验证n=1时通项是否成立,若成立则:an=Sn-Sn-1 (n≥1);若不成立,则通项公式为分段函数.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
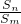 =
=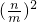 .
.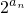 +bn+11≥0成立,求实数b的最小值.
+bn+11≥0成立,求实数b的最小值.