题目内容
已知关于x的方程2sin(x+ )+1-a=0在区间
)+1-a=0在区间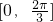 上存在二个根,则实数a的取值范围是________.
上存在二个根,则实数a的取值范围是________.
[2,3)
分析:先求得x+ 的范围,根据题意可得sin(x+
的范围,根据题意可得sin(x+ )=
)=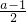 在区间
在区间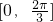 上存在二个根,可得
上存在二个根,可得  ≤
≤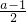 <1,由此求得实数a的取值范围.
<1,由此求得实数a的取值范围.
解答:由x∈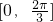 ,则 x+
,则 x+ ∈
∈ ,由关于x的方程2sin(x+
,由关于x的方程2sin(x+ )+1-a=0在区间
)+1-a=0在区间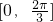 上存在二个根,
上存在二个根,
可得 sin(x+ )=
)=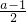 在区间
在区间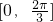 上存在二个根,
上存在二个根,
∴ ≤
≤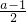 <1,即 1≤a-1<2,解得 2≤a<3,
<1,即 1≤a-1<2,解得 2≤a<3,
故实数a的取值范围是[2,3).
点评:本题主要考查正弦函数的图象,三角函数的最值,做到心中有图,解题才会得心应手,属于中档题.
分析:先求得x+
 的范围,根据题意可得sin(x+
的范围,根据题意可得sin(x+ )=
)=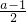 在区间
在区间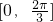 上存在二个根,可得
上存在二个根,可得  ≤
≤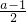 <1,由此求得实数a的取值范围.
<1,由此求得实数a的取值范围.解答:由x∈
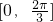 ,则 x+
,则 x+ ∈
∈ ,由关于x的方程2sin(x+
,由关于x的方程2sin(x+ )+1-a=0在区间
)+1-a=0在区间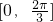 上存在二个根,
上存在二个根,可得 sin(x+
 )=
)=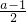 在区间
在区间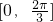 上存在二个根,
上存在二个根,∴
 ≤
≤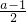 <1,即 1≤a-1<2,解得 2≤a<3,
<1,即 1≤a-1<2,解得 2≤a<3,故实数a的取值范围是[2,3).
点评:本题主要考查正弦函数的图象,三角函数的最值,做到心中有图,解题才会得心应手,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )=a有两个不同的实数解,则实数a的取值范围为
)=a有两个不同的实数解,则实数a的取值范围为 ,2]
,2] ,2]
,2] ,2]
,2]  ,2)
,2) )=a有两个不同的实数解,则实数a的取值范围为
)=a有两个不同的实数解,则实数a的取值范围为


