题目内容
集合M={x|
≥0}，N={x|3（3x-1|（2x+1）≥1}，则集合M、N的关系是
- A.M=N
- B.M?N
- C.M?N
- D.M?N
B
分析：先利用指数函数的性质及分式不等式的解法求出集合A和B，再根据集合之间的关系直接判断选项的正确与否即可．
解答：∵≥0，
∴x≥
，或x＜-
．
∵3（3x-1|（2x+1）≥1，
∴x
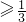或x≤-．
∴M?N．
故选B．
点评：本题主要考查了集合的包含关系判断及应用、指数函数的单调性与特殊点，以及不等式的解法，属于基础题．
分析：先利用指数函数的性质及分式不等式的解法求出集合A和B，再根据集合之间的关系直接判断选项的正确与否即可．
解答：∵
≥0，∴x≥
，或x＜-．∵3（3x-1|（2x+1）≥1，
∴x
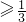或x≤-．∴M?N．
故选B．
点评：本题主要考查了集合的包含关系判断及应用、指数函数的单调性与特殊点，以及不等式的解法，属于基础题．
练习册系列答案
相关题目