题目内容
(14分) 已知a为实数，
（1）求导数
；
（2）若
，求
在[－2，2] 上的最大值和最小值；
（3）若在
和
上都是递增的，求a的取值范围.
(14分)解：⑴由原式得
∴
…………………………………………………….……3分
⑵由
得
,此时有
…...6分
由
得
或x=-1 ……………………………………………………8分
又
所以f(x)在[－2,2]上的最大值为
最小值为
……………………………………………………………10分
⑶解法一:
的图象为开口向上且过点(0,－4)的抛物线,由条件得 
即
∴－2≤a≤2.
所以
的取值范围为[－2,2]…………………………………………….14分
解法二:令即
由求根公式得: 
所以在
和
上非负.
由题意可知,当
或
时, 
≥0,
从而
, 
,
即
解不等式组得－2≤≤2.
∴的取值范围是
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
上的三点，其中点A的坐标为
，BC过椭圆m的中心，且
．（1）求椭圆
的方程；（2）过点
的直线l（斜率存在时）与椭圆m交于两点P，Q，设D为椭圆m与y轴负半轴的交点，且
.求实数t的取值范围．
，g(x)=(lnx-1)ex+x（其中e为自然对数的底数）．（1）判断函数f(x)在
上的单调性；（2）是否存在实数
，使曲线y=g(x)在点x=x0处的切线与y轴垂直? 若存在，求出x0的值；若不存在，请说明理由．（3）若实数m,n满足m>0, n>0,求证：nnem≥mnen.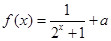
为奇函数。
<0对任意的实数t 恒成立，求k的取值范围.
的左右两个焦点，O为坐标原点，点P 
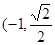）在椭圆上，线段PB与y轴的交点M为线段PB的中点。
是椭圆上异于长轴端点的任一点，对于△ABC，求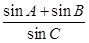
的值。
是奇函数。（1）求a的值；（2）用定义判断该函数的单调性 （3）若对任意的
，不等式
恒成立，求k的取值范围；