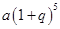题目内容
已知数列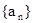 中,
中,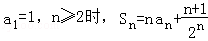
(1)求数列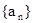 的通项;
的通项;
(2)令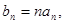 求数列
求数列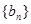 的前n项和Tn.
的前n项和Tn.
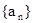 中,
中,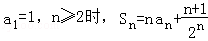
(1)求数列
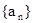 的通项;
的通项;(2)令
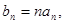 求数列
求数列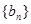 的前n项和Tn.
的前n项和Tn.(1)an= ,(2)Tn=
,(2)Tn=

 ,(2)Tn=
,(2)Tn=

试题分析:(1)本题为由
 求
求 ,当
,当 时,
时, ,约去
,约去 整理得到关于
整理得到关于 的关系式
的关系式 所以
所以

 累加得
累加得 (2)因为
(2)因为 所以数列
所以数列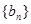 的前n项和为数列
的前n项和为数列 与数列
与数列 前n项和的和. 数列
前n项和的和. 数列 前n项和为
前n项和为 ,而数列
,而数列 前n项和需用错位相减法求解.运用错位相减法求和时需注意三点:一是相减时注意项的符号,二是求和时注意项的个数,三是最后结果需除以
前n项和需用错位相减法求解.运用错位相减法求和时需注意三点:一是相减时注意项的符号,二是求和时注意项的个数,三是最后结果需除以
试题解析:(1)
 ﹣
﹣ ,
,移向整理得出

当n≥2时,an=(an﹣a n﹣1)+(a n﹣1﹣a n﹣2)+…+(a 2﹣a 1)+a1
=
 =1+
=1+ =
= ,n=1时也适合
,n=1时也适合所以an=
 ,
,(2)bn=nan=
 ,
,Tn=
 ﹣(
﹣( )
)令Tn′=
 ,两边同乘以
,两边同乘以 得
得 Tn′=
Tn′=
两式相减得出
 Tn′=
Tn′= =
= =
=
Tn′=

所以Tn=
 ﹣(
﹣( )
)=


 求
求 ,错位相减法求和
,错位相减法求和
练习册系列答案
相关题目
 (n∈N*),求设数列{bn}的前n项和Tn.
(n∈N*),求设数列{bn}的前n项和Tn.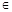 N*,都有
N*,都有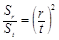 .
.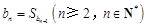 ,求证:数列
,求证:数列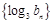 为等比数列;
为等比数列;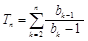 .
. 中,
中, .对任意的
.对任意的 ,函数
,函数


 满足
满足 .
. 的前
的前 项和
项和 .
.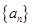 的通项公式为
的通项公式为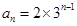 ,则由此数列的偶数项所组成的新数列的前
,则由此数列的偶数项所组成的新数列的前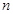 项和
项和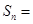 ( )
( ) 



 满足公比
满足公比 ,
, ,且数列
,且数列 ,则
,则 的所有可能取值之和为_______________.
的所有可能取值之和为_______________. 的前
的前 项和为
项和为 ,若
,若 =3,则
=3,则 =
=  元的一年定期储蓄。若年利率为
元的一年定期储蓄。若年利率为 保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.