题目内容
14.($\frac{x}{\sqrt{y}}$-$\frac{y}{\sqrt{x}}$)6的展开式中,x3的系数等于( )| A. | -15 | B. | 15 | C. | 20 | D. | -20 |
分析 写出二项展开式的通项公式,由x的指数等于3求出r的值,即可求出答案.
解答 解:($\frac{x}{\sqrt{y}}$-$\frac{y}{\sqrt{x}}$)6的展开式中,通项公式为
Tr+1=${C}_{6}^{r}$•${(\frac{x}{\sqrt{y}})}^{6-r}$•${(-\frac{y}{\sqrt{x}})}^{r}$=(-1)r•${C}_{6}^{r}$•${x}^{6-\frac{3r}{2}}$•${y}^{\frac{3r}{2}-3}$,
由6-$\frac{3r}{2}$=3,得r=2;
∴($\frac{x}{\sqrt{y}}$-$\frac{y}{\sqrt{x}}$)6的展开式中,x3的系数为(-1)2•${C}_{6}^{2}$=15.
故选:B.
点评 本题考查了二项式系数的性质应用问题,解题的关键是灵活应用二项展开式的通项公式,是基础题.

练习册系列答案
相关题目
4.阅读如图所示的程序框图,运行相应的程序,输出的n的值等于( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
9.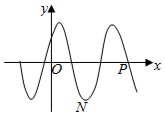 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )| A. | $[\frac{π}{8},\frac{5π}{8}]$ | B. | $[-\frac{7π}{8},-\frac{3π}{8}]$ | C. | $[\frac{9π}{4},\frac{21π}{8}]$ | D. | $[\frac{9π}{8},\frac{33π}{8}]$ |
3.某程序框图如图所示,运行该程序,那么输出k的值是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( )
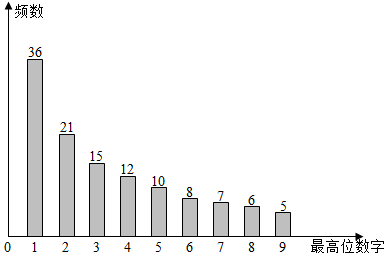

| A. | P=lg(1+$\frac{1}{d}$) | B. | P=$\frac{1}{d+2}$ | C. | P=$\frac{{(d-5)}^{2}}{120}$ | D. | P=$\frac{3}{5}$×$\frac{1}{{2}^{d}}$ |