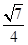题目内容
关于直线 、
、 与平面
与平面 、
、 ,有下列四个命题:
,有下列四个命题:
① 且
且 ,则
,则 ; ②
; ② 且
且 ,则
,则 ;
;
③ 且
且 ,则
,则 ; ④
; ④ 且
且 ,则
,则 .
.
其中假命题的序号是:( )
| A.①、② | B.③、④ | C.②、③ | D.①、④ |
D
解析试题分析:由题意两条直线m,n与两个平面 、
、
由于若 且
且 ,不能确定两条直线的位置关系,故①是假命题;
,不能确定两条直线的位置关系,故①是假命题;
由于若 且且
且且 ,可以确定两条直线垂直,故②是真命题;
,可以确定两条直线垂直,故②是真命题;
由于若 且
且 ,可以判断两条直线垂直,故③是真命题;
,可以判断两条直线垂直,故③是真命题;
由于 且
且 不能确定两条直线的位置关系,故④是假命题;
不能确定两条直线的位置关系,故④是假命题;
考点:空间中直线与直线之间的位置关系.
点评:本题的考点是间中直线一直线之间的位置关系,考查了线线平行与线线垂直的条件,解题的关键是理
解题意,有着较强的空间立体感知能力,本题考查了空间想像能力,推理判断的能力,是高考中常见题型,
其特点是涉及到的知识点多,知识容量大,因此备受高考命题者青睐.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
若直线上有两个点在平面外,则( )
| A.直线上至少有一个点在平面内 |
| B.直线上有无穷多个点在平面内 |
| C.直线上所有点都在平面外 |
| D.直线上至多有一个点在平面内 |
如图,在长方体 中,
中,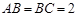 ,
, ,则异面直线
,则异面直线 与
与 所成的角为 ( )
所成的角为 ( )
A. | B.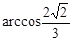 |
C.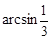 | D. |
设、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若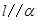 , , ,则 ,则 | D.若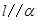 , , ,则 ,则 |
已知直线 ,平面
,平面 ,且
,且 ,给出四个命题: ①若
,给出四个命题: ①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;③若
;③若 ,则
,则 ∥m;④若
∥m;④若 ∥m,则
∥m,则 .其中真命题的个数是
.其中真命题的个数是
| A.4 | B.3 | C.2 | D.1 |
在三棱锥 中,
中, ,
, 是等腰直角三角形,
是等腰直角三角形,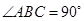 ,
, 为
为 中点. 则
中点. 则 与平面
与平面 所成的角等于( )
所成的角等于( )
A. | B. | C. | D. |
已知m、n是两条不同的直线, 、
、 、
、 是三个不同的平面,下列命题中错误的是( )
是三个不同的平面,下列命题中错误的是( )
A.若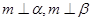 则 则 ∥ ∥ |
B.若 ∥ ∥ , , ∥ ∥ 则 则 ∥ ∥ |
C.若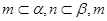 ∥n则 ∥n则 ∥ ∥ |
D.若m、n是异面直线,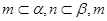 ∥ ∥ ,n∥ ,n∥ 则 则 ∥ ∥ |
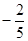
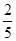
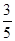
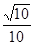
 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,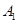 在底面
在底面 上的射影为
上的射影为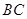 的中点D,则异面直线AD与
的中点D,则异面直线AD与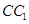 所成的角的余弦值为( )
所成的角的余弦值为( )