题目内容
如图,在长方体 中,
中,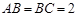 ,
, ,则异面直线
,则异面直线 与
与 所成的角为 ( )
所成的角为 ( )
A. | B.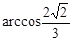 |
C.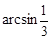 | D. |
D
解析试题分析:根据题意,由于长方体 中,
中,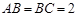 ,
, ,,将
,,将 平移到
平移到 ,则异面直线
,则异面直线 与
与 所成的角,即为
所成的角,即为 与
与 所成的夹角,故结合余弦定理可知,余弦值为
所成的夹角,故结合余弦定理可知,余弦值为 ,那么可知正切值为
,那么可知正切值为 ,故可知该角的大小为
,故可知该角的大小为
 ,选D.
,选D.
考点:异面直线所角
点评:本题主要考查异面直线所角的基本求法,若所成的角在直角三角形中,则用三角函数的定义,若在一般三角形中则用余弦定理.

练习册系列答案
相关题目
设 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
如图,已知长方体 中,
中,  ,
, ,则二面角
,则二面角 的余弦值为
的余弦值为
A. | B. | C. | D. |
已知 是两个不同的平面,
是两个不同的平面, 是不同的直线,下列命题不正确的是
是不同的直线,下列命题不正确的是
A.若 则 则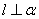 |
B.若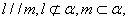 则 则 |
C.若 则 则 |
D.若 ,则 ,则 |
点 到直线
到直线 的距离为( )
的距离为( )
| A.2 | B.1 | C. | D. |
下列关于直线l,m与平面α,β的说法,正确的是 ( )
A.若l β且α⊥β,则l⊥α β且α⊥β,则l⊥α | B.若l⊥β且α∥β,则l⊥α |
| C.若l⊥β且α⊥β,则l∥α | D.若α β=m,且l∥m, 则l∥α β=m,且l∥m, 则l∥α |
关于直线 、
、 与平面
与平面 、
、 ,有下列四个命题:
,有下列四个命题:
① 且
且 ,则
,则 ; ②
; ② 且
且 ,则
,则 ;
;
③ 且
且 ,则
,则 ; ④
; ④ 且
且 ,则
,则 .
.
其中假命题的序号是:( )
| A.①、② | B.③、④ | C.②、③ | D.①、④ |
已知两条不同直线 和
和 及平面
及平面 ,则直线
,则直线 的一个充分条件是 ( )
的一个充分条件是 ( )
A. 且 且 | B. 且 且 |
C. 且 且 | D. 且 且 |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 , , , , ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , , , ,则 ,则 |
D.若 , , , , ,则 ,则 |