题目内容

如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD于E,AF⊥DB于F.求证: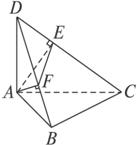

(1)EF⊥DC;

(2)平面DBC⊥平面AEF.

解析:(1)要证线线垂直,先证线面垂直:要证EF⊥DC,应先证EF垂直于DC所在的某一个平面,或证CD垂直于EF所在的某一个平面.

(2)要证面面垂直,先找线面垂直:要证平面DBC⊥平面AEF,应在平面DBC中找一条直线垂直于平面AEF,或在平面AEF中找一条直线垂直于平面DBC.

证明:(1)∵AD⊥平面ABC,

∴AD⊥BC.

又BC⊥AB,∴BC⊥平面ABD.

∴BC⊥AF.又BD⊥AF,

∴AF⊥平面BCD.

∴AF⊥CD.

又AE⊥CD,

∴CD⊥平面AEF.

∴CD⊥EF.

(2)在(1)中已证AF⊥平面BCD,

∴平面AEF经过平面BCD的一条垂线AF.

∴平面DBC⊥平面AEF.

小结:把第二问的条件改为AF⊥BD,E为CD上的任意一点,也能得到平面DBC⊥平面AEF.

练习册系列答案
相关题目
精英家教网如图，在空间四边形OABC中，M，G分别是BC，AM的中点，设
OA
=
a
，
OB
=
b
，
OC
=
c
．
（1）用基底{
a
 ， 
b
 ，
c
}表示向量
OG
；
（2）若|
a
|=|
b
|=|
c
|=
3
，且
a
与
b
、
c
夹角的余弦值均为
1
3
，
b
与
c
夹角为60°，求|
OG
|．
如图，在空间四边形ABCD中，点E、H分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且
CF
CB
=
CG
CD
=
2
3
，则（　　）
如图，在空间四边形OABC中，已知E是线段BC的中点，G为AE的中点，若
OA
，
OB
，
OC
分别记为
a
，
b
，
c
，则用
a
，
b
，
c
表示
OG
的结果为
OG
=
1
2
a
+
1
4
b
+
1
4
c
1
2
a
+
1
4
b
+
1
4
c
．
如图，在空间四边形PABC中，PA⊥面ABC，AC⊥BC，若点A在PB、PC上的射影分别是E、F，求证：EF⊥PB.

如图，在空间四边形ABCD中，点E、H分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且＝＝，则（　　）

（A）EF与GH互相平行

（B）EF与GH异面

（C）EF与GH的交点M可能在直线AC上，也可能不在直线AC上

（D）EF与GH的交点M一定在直线AC上

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网