题目内容
已知数列
,
,
,…,
,…的前n项和为Sn.
(Ⅰ)计算S1,S2,S3,S4;
(Ⅱ)根据(Ⅰ)所得到的计算结果,猜想Sn的表达式,不必证明.
| 2 |
| 1×3 |
| 2 |
| 3×5 |
| 2 |
| 5×7 |
| 2 |
| (2n-1)(2n+1) |
(Ⅰ)计算S1,S2,S3,S4;
(Ⅱ)根据(Ⅰ)所得到的计算结果,猜想Sn的表达式,不必证明.
分析:(I)由已知中数列通项公式为an=
,依次代入可求出S1,S2,S3,S4;
(Ⅱ)根据(Ⅰ)所得到的计算结果,分析结果中分子和分母的变化规律,可得Sn的表达式
| 2 |
| (2n-1)(2n+1) |
(Ⅱ)根据(Ⅰ)所得到的计算结果,分析结果中分子和分母的变化规律,可得Sn的表达式
解答:解:(I)∵数列
,
,
,…,
,…的前n项和为Sn.
∴S1=
=
,
S2=
+
=
,
S3=
+
+
=
,
S4=
+
+
+
=
,
(II)由(I)中
S1=
=
,
S2=
=
,
S3=
=
,
S4=
=
,
…
由此猜想Sn=
| 2 |
| 1×3 |
| 2 |
| 3×5 |
| 2 |
| 5×7 |
| 2 |
| (2n-1)(2n+1) |
∴S1=
| 2 |
| 1×3 |
| 2 |
| 3 |
S2=
| 2 |
| 1×3 |
| 2 |
| 3×5 |
| 4 |
| 5 |
S3=
| 2 |
| 1×3 |
| 2 |
| 3×5 |
| 2 |
| 5×7 |
| 6 |
| 7 |
S4=
| 2 |
| 1×3 |
| 2 |
| 3×5 |
| 2 |
| 5×7 |
| 2 |
| 7×9 |
| 8 |
| 9 |
(II)由(I)中
S1=
| 2 |
| 3 |
| 2×1 |
| 2×1+1 |
S2=
| 4 |
| 5 |
| 2×2 |
| 2×2+1 |
S3=
| 6 |
| 7 |
| 2×3 |
| 2×3+1 |
S4=
| 8 |
| 9 |
| 2×4 |
| 2×4+1 |
…
由此猜想Sn=
| 2n |
| 2n+1 |
点评:本题考查的知识点是数列求和,归纳推理,难度不大,其中(II)中要注意分析(I)中结论分子和分母的变化规律

练习册系列答案
相关题目
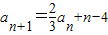 ,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.