题目内容
17.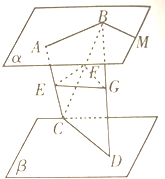 如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.
如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.
分析 由三角形中位线定理得EF∥AB,FG∥CD,从而得到EF∥α,FG∥β,由此能证明平面EFG∥α∥β.
解答 证明:∵平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,
E、F、G分别是AC、CB、BD的中点,
∴EF∥AB,FG∥CD,
∵EF?平面α,AB?平面α,∴EF∥α,
∵FG?平面β,CD?平面β,∴FG∥β,
∵α∥β,∴EF∥α,FG∥α,EF∥β,FG∥β,
∵EF∩FG=F,
∴平面EFG∥α∥β.
点评 本题考查平面平行的证明,是中档题,解题时要认真审题,注意三角形中位线定理、平行公理的合理运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8.若x∈R,且满足$\frac{x}{4}+\frac{1}{x}$=sinθ,则θ的值等于( )
| A. | kπ+$\frac{π}{2}$(k∈Z) | B. | kπ(k∈Z) | C. | 2kπ+$\frac{π}{2}$(k∈Z) | D. | $\frac{1}{2}kπ$(k∈Z) |
6.在($\sqrt{x}-\frac{2}{\sqrt{x}}$)n的展开式中,偶数项的二次项系数为64,则展开式共有( )
| A. | 6项 | B. | 7项 | C. | 8项 | D. | 9项 |
20.经过A(-2,0),B(-5,3)两点的直线的倾斜角( )
| A. | 45° | B. | 135° | C. | 90° | D. | 60° |
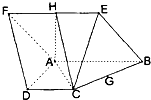 如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.
如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点. 如图,抛物线的方程为y2=2px(p>0),F为该抛物线的焦点,A是该抛物线的准线与x轴的交点,M是抛物线上一点,且满足MA⊥MF.
如图,抛物线的方程为y2=2px(p>0),F为该抛物线的焦点,A是该抛物线的准线与x轴的交点,M是抛物线上一点,且满足MA⊥MF.