题目内容
已知复数 ,函数
,函数 图象的一个对称中心可以是( )
图象的一个对称中心可以是( )A.

B.

C.

D.

【答案】分析:根据两个复数相等的充要条件求出a 和 b 的值,得到函数f(x)的解析式,由 3x+ =kπ+
=kπ+ ,或3x+
,或3x+ =kπ,
=kπ,
k∈z,求得函数f(x)的对称中心 的横坐标x,纵坐标为 1,从而得到函数f(x)的对称中心.
解答:解:∵复数 =
= =
= =3+i,∴a=3,b=1.
=3+i,∴a=3,b=1.
故函数 =2tan(3x+
=2tan(3x+ )+1.
)+1.
令 3x+ =kπ+
=kπ+ 得 x=
得 x= ,令 3x+
,令 3x+ =kπ,得 x=
=kπ,得 x= -
- ,k∈z.
,k∈z.
故函数f(x)的对称中心为 ( ,1)或 (
,1)或 ( -
- ,1),k∈z,
,1),k∈z,
故选 D.
点评:本题考查复数代数形式的混合运算,两个复数相等的充要条件,正切函数的对称中心,得到函数f(x)的解析式为
2tan(3x+ )+1,是解题的关键.
)+1,是解题的关键.
 =kπ+
=kπ+ ,或3x+
,或3x+ =kπ,
=kπ,k∈z,求得函数f(x)的对称中心 的横坐标x,纵坐标为 1,从而得到函数f(x)的对称中心.
解答:解:∵复数
 =
= =
= =3+i,∴a=3,b=1.
=3+i,∴a=3,b=1.故函数
 =2tan(3x+
=2tan(3x+ )+1.
)+1.令 3x+
 =kπ+
=kπ+ 得 x=
得 x= ,令 3x+
,令 3x+ =kπ,得 x=
=kπ,得 x= -
- ,k∈z.
,k∈z.故函数f(x)的对称中心为 (
 ,1)或 (
,1)或 ( -
- ,1),k∈z,
,1),k∈z,故选 D.
点评:本题考查复数代数形式的混合运算,两个复数相等的充要条件,正切函数的对称中心,得到函数f(x)的解析式为
2tan(3x+
 )+1,是解题的关键.
)+1,是解题的关键. 
练习册系列答案
相关题目
 ,函数
,函数 图象的一个对称中心可以是
图象的一个对称中心可以是



 图象的一个对称中心是
图象的一个对称中心是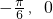 )
) )
) )
) ,函数
,函数 图象的一个对称中心是( )
图象的一个对称中心是( ) )
) )
) )
) ,函数
,函数 图象的一个对称中心是
图象的一个对称中心是 ) B. (
) B. ( )
C.(
)
C.( ) D.(
) D.( )
)