题目内容
已知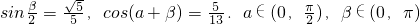
．求cosβ和sinβ．
解：∵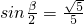
，
∴cosβ=1-2sin2
=
∵β∈（0，π），
∴sinβ=
=
∵0＜α＜
，
∴0＜α+β＜
∵cos（α+β）=
＞0
∴0＜α+β＜
∴sin（α+β）=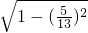
=
，
∴sinα=sin[α+β）-β]=sin（α+β）cosβ-cos（α+β）sinβ=
分析：先根据二倍角公式求得cosβ的值，进而利用同角三角函数的基本关系和β的范围求得sinβ的值，进而根据α，β和kcos（α+β）的值确定α+β的范围，进而利用同角三角函数的基本关系求得sin（α+β）的值，进而利用两角和公式求得cosβ的值．
点评：本题主要考查了两角和与差的正弦函数，二倍角公式的应用和同角三角函数的基本关系的应用．考查了学生的运算能力和基础知识的综合运用．
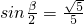，∴cosβ=1-2sin2
=∵β∈（0，π），
∴sinβ=
=∵0＜α＜
，∴0＜α+β＜
∵cos（α+β）=
＞0∴0＜α+β＜
∴sin（α+β）=
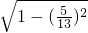=，∴sinα=sin[α+β）-β]=sin（α+β）cosβ-cos（α+β）sinβ=
分析：先根据二倍角公式求得cosβ的值，进而利用同角三角函数的基本关系和β的范围求得sinβ的值，进而根据α，β和kcos（α+β）的值确定α+β的范围，进而利用同角三角函数的基本关系求得sin（α+β）的值，进而利用两角和公式求得cosβ的值．
点评：本题主要考查了两角和与差的正弦函数，二倍角公式的应用和同角三角函数的基本关系的应用．考查了学生的运算能力和基础知识的综合运用．
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
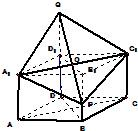如图，已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形，Q是侧棱DD1（DD1＞
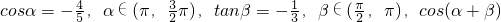，求cos（α+β）．
，求cos（α+β）．
，求cos（α+β）．