题目内容
设△ABC的内角A,B,C所对的边长分别为a,b,c,且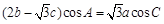 .
.
(1)求角 的大小;
的大小;
(2)若角 ,
, 边上的中线
边上的中线 的长为
的长为 ,求
,求 的面积.
的面积.
(1) .(2)
.(2)
解析试题分析:(1)∵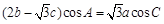 ,
,
∴ . 2分
. 2分
即 .
.
∴ . 4分
. 4分
则 ,∴
,∴ , 6分因为
, 6分因为 则
则 . 7分
. 7分
(2)由(1)知 ,所以
,所以 ,
, ,
,
设 ,则
,则 ,又
,又 
在 中由余弦定理得
中由余弦定理得 10分
10分
即
解得 12分
12分
故 14分
14分
考点:本题主要考查正弦定理、余弦定理的应用,和差倍半的三角函数公式
点评:典型题,涉及三角形问题,往往要从边或角两方面加以分析,探寻解题思路,求角时,应优先考虑求角的余弦值,以避免不必要的讨论。本题(2)利用函数方程思想,应用余弦定理得到关于三角形边长的方程,进一步确定三角形面积。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 且
且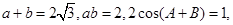
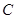 度数 (2)
度数 (2) 的长 (3)△ABC的面积
的长 (3)△ABC的面积 中,角
中,角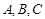 所对的边分别为
所对的边分别为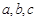 ,若
,若 。
。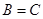 ;
;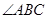 的平分线交
的平分线交 于
于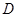 ,且
,且 ,求
,求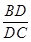 的值。
的值。 .
. 中,已知
中,已知 ,
, ,
, , 求
, 求 、
、 及
及 。
。 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知
 的值。
的值。 中,
中,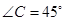 ,
, 为
为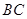 中点,
中点,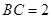 .记锐角
.记锐角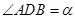 .且满足
.且满足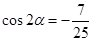 .
.
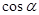 ;
;  =(sinA,b+c),
=(sinA,b+c),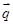 =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足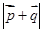 =
=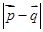 (Ⅰ)求角B的大小;(Ⅱ)设
(Ⅰ)求角B的大小;(Ⅱ)设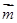 =(sin(C+
=(sin(C+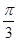 ),
), ),
), 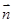 =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值. 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10