Question

已知集合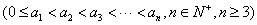，具有性质：对任意的，至少有一个属于.

（Ⅰ）分别判断集合与是否具有性质；

（Ⅱ）求证：①；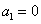

②；

（Ⅲ）当或时集合中的数列是否一定成等差数列?说明理由.

Answer 1

解：（Ⅰ）集合具有性质，

，，集合不具有性质.

（Ⅱ）由已知，，

则，仍由知；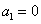

，，

 

将上述各式两边相加得

，即；

（Ⅲ）当时，集合中的数列一定是等差数列.

由（Ⅱ）知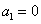，且，

故，而这里，反之若不然

这与集合中元素互异矛盾，只能，即

成等差数列.  

当时，集合中的元素不一定是等差数列.

如，中元素成等差数列，

又如，中元素不成等差数列；

当5时，集合中的元素一定成等差数列

证明：

令①②

②①有，且由①

，  

，

又，

成等差数列.