Question

【题目】已知椭圆 经过点 ,离心率为 ,左、右焦点分别为 ．
（1）求椭圆的方程;
（2）若直线 与椭圆交于A,B两点,与以 为直径的圆交于C,D两点,求 的值．

Answer 1

【答案】
（1）由题设知
解得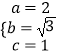
∴椭圆的方程为 ＋ ＝1.
故答案为：.
（2）由题设,以F1F2为直径的圆的方程为x2＋y2＝1,
∴圆心到直线l的距离d＝ ,
∴|CD|＝2 ＝ .
设A(x1,y1),B(x2,y2),
由 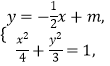得4x2-4x+8＝0.
由根与系数的关系可得x1＋x2＝1,x1x2＝-2.
∴|AB|＝ ,则 ＝ .
故答案为：.
【解析】（1）将已知条件中的点及离心率代入，即可求出椭圆的方程。
（2）根据已知条件联立得出方程式后，再根据根与系数的关系即可求出。