题目内容
已知椭圆 的焦点分别为F1,F2,P为椭圆上一点,且∠F1PF2=90°,则点P的纵坐标可以是( )
的焦点分别为F1,F2,P为椭圆上一点,且∠F1PF2=90°,则点P的纵坐标可以是( )A.

B.

C.

D.

【答案】分析:先根据椭圆的标准方程确定椭圆的几何量,再利用P为椭圆上一点,且∠F1PF2=90°,建立方程组,从而可求三角形的面积,进而利用等面积可求点P的纵坐标.
解答:解:设|PF1|=m,|PF2|=n,
椭圆 中,a2=4,b2=1,c2=3,
中,a2=4,b2=1,c2=3,
∴
∵P为椭圆上一点,且∠F1PF2=90°,
∴
∴2mn=4
∴
设点P的纵坐标为y,则
∴
故选B.
点评:本题以椭圆的标准方程为载体,考查椭圆的性质,考查等面积的运用,属于基础题.
解答:解:设|PF1|=m,|PF2|=n,
椭圆
 中,a2=4,b2=1,c2=3,
中,a2=4,b2=1,c2=3,∴

∵P为椭圆上一点,且∠F1PF2=90°,
∴

∴2mn=4
∴

设点P的纵坐标为y,则

∴

故选B.
点评:本题以椭圆的标准方程为载体,考查椭圆的性质,考查等面积的运用,属于基础题.

练习册系列答案
相关题目
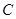 的焦点分别为
的焦点分别为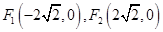 ,且过点
,且过点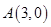 .
.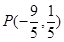 为椭圆
为椭圆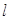 交椭圆
交椭圆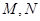 两点,且
两点,且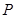 为线段
为线段 的中点,求直线
的中点,求直线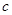 的焦点分别为
的焦点分别为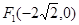 、
、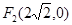 ,长轴长为6,设直线
,长轴长为6,设直线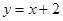 交椭圆
交椭圆 的面积。
的面积。 的焦点分别为F1,F2,b=4,离心率
的焦点分别为F1,F2,b=4,离心率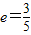 ,过F1的直线交椭圆于A,B两点,则△ABF2的周长为( )
,过F1的直线交椭圆于A,B两点,则△ABF2的周长为( )