题目内容
【题目】设![]() ,
,![]() 为正整数,一个正整数数列
为正整数,一个正整数数列![]() 满足
满足![]() .对
.对![]() ,定义集合
,定义集合![]() .数列
.数列![]() 中的
中的![]() 是集合
是集合![]() 中元素的个数.
中元素的个数.
(1)若数列![]() 为5,3,3,2,1,1,写出数列
为5,3,3,2,1,1,写出数列![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 为公比为
为公比为![]() 的等比数列,求
的等比数列,求![]() ;
;
(3)对![]() ,定义集合
,定义集合![]() ,令
,令![]() 是集合
是集合![]() 中元素数的个数.求证:对
中元素数的个数.求证:对![]() ,均有
,均有![]() .
.
【答案】(1)数列![]() 为
为![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)根据题意得出求出![]() ,即可得出数列
,即可得出数列![]() ;
;
(2)根据题意得出![]() ,从而写出数列
,从而写出数列![]() ,假设数列
,假设数列![]() 中有
中有![]() 个
个![]() ,
,![]() 个
个![]() ,…,
,…,![]() 个
个![]() ,
,![]() 个
个![]() ,结合题设条件证明
,结合题设条件证明![]() ,利用等比数列的求和公式即可得出
,利用等比数列的求和公式即可得出![]() ;
;
(3)利用(2)中结论得出![]() ,接下来证明对
,接下来证明对![]() ,即可得出.
,即可得出.
(1)![]()
![]() 数列
数列![]() 为
为![]()
(2)由题意知![]() ,则
,则![]()
因为数列![]() 为公比为
为公比为![]() 的等比数列,所以数列
的等比数列,所以数列![]() 为
为![]()
假设数列![]() 中有
中有![]() 个
个![]() ,
,![]() 个
个![]() ,…,
,…,![]() 个
个![]() ,
,![]() 个
个![]()
所以![]()
由题意可知
![]()
![]()
![]()
…
![]()
…
![]()
所以![]()
所以
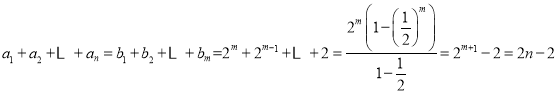
(3)对![]() ,
,![]() 表示数列
表示数列![]() 中大于等于
中大于等于![]() 的个数,即
的个数,即![]()
由(2)知
![]()
![]()
![]()
…
![]()
并且![]()
所以![]()
设![]() ,则
,则![]() ,即
,即![]() ,从而
,从而![]()
故![]()
从而![]() ,故
,故![]() ,而
,而![]() ,故有
,故有![]()
设![]() ,即
,即![]() ,根据集合
,根据集合![]() 的定义,有
的定义,有![]()
由![]() 知,
知,![]() ,由
,由![]() 的定义可得
的定义可得![]()
而由![]() ,故
,故![]()
由此,对![]() ,均有
,均有![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目