题目内容
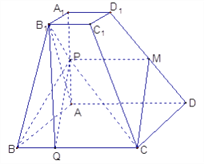
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
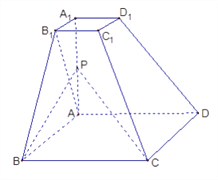
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析;(Ⅱ) ![]()
【解析】试题分析:(Ⅰ)由面面垂直的判定定理证明;(Ⅱ)取![]() 中点为M,连PM,CM,在BC边上取点Q,使
中点为M,连PM,CM,在BC边上取点Q,使![]() ,证明四边形
,证明四边形![]() 为平行四边形,得出
为平行四边形,得出![]() ,得到
,得到![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积时,先计算
的体积时,先计算![]() 的面积,再由等体积法求出体积.
的面积,再由等体积法求出体积.
试题解析:(Ⅰ)∵![]() ⊥面ABCD,BC
⊥面ABCD,BC![]() 面ABCD∴
面ABCD∴![]() ⊥BC
⊥BC
∵ABCD是正方形,∴AB⊥BC∴BC⊥面![]()
∵![]()
![]() 面
面![]() ∴
∴![]() ⊥BC
⊥BC
![]()
所以![]() ≌
≌![]() ,可证得
,可证得![]() ⊥BP
⊥BP
∵BP∩BC=B,∴![]() ⊥面PBC
⊥面PBC
(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() ,在
,在![]() 边上取一点
边上取一点![]() ,
,
使![]() ,则
,则![]() //
// ![]() ,
,
所以:PQCM为平行四边形, ![]() //
// ![]()
所以:PQ//面![]() ,
,
∵PQCM为平行四边形,∴CQ=PM=![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.