题目内容
甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计后,得出如下的列联表:
(1)画出列联表的二维条形图,并通过条形图判断成绩是否与班级有关;
(2)利用列联表的独立性检验估计,认为“成绩与班级有关系”犯错误的概率是多少?是否有99%的把握认为“成绩与班级有关系”
附表:
| 优秀 | 不优秀 | 总计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
(2)利用列联表的独立性检验估计,认为“成绩与班级有关系”犯错误的概率是多少?是否有99%的把握认为“成绩与班级有关系”
附表:
| P(K2≥k0) | 0.10 | 0.010 | 0.001 |
| k0 | 2.706 | 6.635 | 10.828 |
分析:(1)根据题中所给的数据,画出列联表的二维条形图,从图中可以看出成绩优秀与班级没有明显关系,
(2)把列联表中所给的数据代入代入求观测值的公式,运算出最后结果15.88,把所得的结果同观测值表中的数值进行比较,得到有99.9%的把握认为成绩与班级有关系
(2)把列联表中所给的数据代入代入求观测值的公式,运算出最后结果15.88,把所得的结果同观测值表中的数值进行比较,得到有99.9%的把握认为成绩与班级有关系
解答:解:(1)画出列联表的二维条形图如下图所示,从图中可以看出成绩优秀与班级没有明显关系,

(2)假设成绩优秀和班级无关系,则有a=10,b=35,c=7,d=38,a+b=45,c+d=45,a+c=17,b+d=73,n=90,
代入k2公式得到k2=
≈0.653,
由于k2≈0.653<6.635,
所以没有99%的把握认为“成绩优秀与班级有关系”

(2)假设成绩优秀和班级无关系,则有a=10,b=35,c=7,d=38,a+b=45,c+d=45,a+c=17,b+d=73,n=90,
代入k2公式得到k2=
| n(ad-bc)2 |
| (a+b)(b+d)(c+d)(a+c) |
由于k2≈0.653<6.635,
所以没有99%的把握认为“成绩优秀与班级有关系”
点评:本题考查独立性检验的应用,利用图形可以判断两个变量之间是否有关系,但是要想知道两个变量之间的有关或无关的精确的可信程度,只有利用独立性检验的有关计算,才能做出判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
.甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下列联表:
|
|
优秀 |
不优秀 |
合计 |
|
甲班 |
10 |
35 |
45 |
|
乙班 |
7 |
38 |
45 |
|
合计 |
17 |
73 |
90 |
利用独立性检验估计,你认为推断“成绩与班级有关系”错误的概率介于( )
A.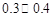 B.
B.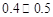 C.
C.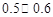 D.
D.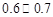
甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下列联表:
| 优秀 | 不优秀 | 总计 |
甲班 | 10 | 35 | 45 |
乙班 | 7 | 38 | 45 |
总计 | 17 | 73 | 90 |
利用列联表的独立性检验估计,认为“成绩与班级有关系”犯错误的概率是多少?
甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计后,得出如下的列联表:
(1)画出列联表的二维条形图,并通过条形图判断成绩是否与班级有关;
(2)利用列联表的独立性检验估计,认为“成绩与班级有关系”犯错误的概率是多少?是否有99%的把握认为“成绩与班级有关系”
附表:
| 优秀 | 不优秀 | 总计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
(2)利用列联表的独立性检验估计,认为“成绩与班级有关系”犯错误的概率是多少?是否有99%的把握认为“成绩与班级有关系”
附表:
| P(K2≥k) | 0.10 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
 (其中
(其中 )
)










