题目内容
甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下列联表:
| 优秀 | 不优秀 | 总计 |
甲班 | 10 | 35 | 45 |
乙班 | 7 | 38 | 45 |
总计 | 17 | 73 | 90 |
利用列联表的独立性检验估计,认为“成绩与班级有关系”犯错误的概率是多少?
分析:求出χ2,然后查表求概率.
解:假设成绩优秀与班级无关系,则有a=10,b=35,c=7,d=38,a+b=45,c+d=45,a+c=17,b+d=73,n=90,代入χ2公式得χ2的值.
χ2=![]() =
=![]() =0.653,
=0.653,
由于χ2=0.653<2.706,所以没有充分证据说明优秀与班级有关系,认为成绩与班级有关系犯错误的概率为99%.
绿色通道
从本题可知,学习成绩主要取决于个人努力的结果,与所在班级的关系不大.所以同学们要从自身找原因,不要强调外界环境.
利用公式计算χ2的值时,一定要计算准确.

练习册系列答案
相关题目
.甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下列联表:
|
|
优秀 |
不优秀 |
合计 |
|
甲班 |
10 |
35 |
45 |
|
乙班 |
7 |
38 |
45 |
|
合计 |
17 |
73 |
90 |
利用独立性检验估计,你认为推断“成绩与班级有关系”错误的概率介于( )
A.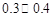 B.
B.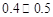 C.
C.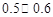 D.
D.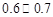
甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计后,得出如下的列联表:
(1)画出列联表的二维条形图,并通过条形图判断成绩是否与班级有关;
(2)利用列联表的独立性检验估计,认为“成绩与班级有关系”犯错误的概率是多少?是否有99%的把握认为“成绩与班级有关系”
附表:
| 优秀 | 不优秀 | 总计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
(2)利用列联表的独立性检验估计,认为“成绩与班级有关系”犯错误的概率是多少?是否有99%的把握认为“成绩与班级有关系”
附表:
| P(K2≥k) | 0.10 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
 (其中
(其中 )
)










