题目内容
已知a∈(0,2),当a为何值时,直线l1:ax-2y=2a-4与l2:2x+a2y=2a2+4及坐标轴围成的平面区域的面积最小?
分析:求出四边形的A、B、C的顶点坐标,再运用面积公式合理求解.
解答:解:直线l1交y轴于A(0,2-a),直线l2交x轴于C(a2+2,0),
l1与l2交于点B(2,2).
则四边形AOCB的面积为S=S△AOB+S△OCB=
•(2-a)•2+
(a2+2)•2=a2-a+4=(a-
)2+
,
当a=
时,S最小.
因此使四边形面积最小时a的值为
.

l1与l2交于点B(2,2).
则四边形AOCB的面积为S=S△AOB+S△OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
当a=
| 1 |
| 2 |
因此使四边形面积最小时a的值为
| 1 |
| 2 |
点评:本题考查两直线的交点坐标的求法和四边形面积的求法,解题时要认真审题,仔细解答,注意配方法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
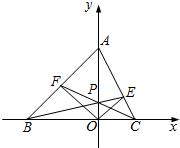 如图,在平面直角坐标系xOy中,已知A(0,2),B(-2,0),C(1,0),P(0,p)(0<p<2),直线BP与AC交于点E,直线CP与AB交于点F,若OE⊥OF,则实数p的值是
如图,在平面直角坐标系xOy中,已知A(0,2),B(-2,0),C(1,0),P(0,p)(0<p<2),直线BP与AC交于点E,直线CP与AB交于点F,若OE⊥OF,则实数p的值是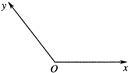 如图,在平面斜坐标系xOy中,∠xOy=135°.斜坐标定义:如果
如图,在平面斜坐标系xOy中,∠xOy=135°.斜坐标定义:如果