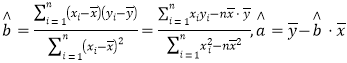题目内容
【题目】以直角坐标系的原点
为极点， 
轴正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线
的参数方程为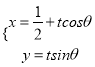
，（ 
为参数， 
），曲线
的极坐标方程为
.
（1）求曲线
的直角坐标方程；
（2）设直线
与曲线
相交于
， 
两点，当
变化时，求
的最小值.
【答案】（1）
（2）2
【解析】试题分析：（1）本问考查极坐标与直角坐标互化公式，根据
可得
，所以曲线C的直角坐标方程为
；（2）本问考查直线参数方程标准形式下的几何意义，即将直线参数方程的标准形式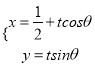
，代入到曲线C的直角坐标方程，得到关于t的一元二次方程，设
两点对应的参数分别为
，列出
， 
， 
，于是可以求出
的最小值.
试题解析：（I）由
由，得
曲线 
的直角坐标方程为
（II）将直线
的参数方程代入，得
设
两点对应的参数分别为
则
， 
，
当
时， 
的最小值为2.
练习册系列答案
相关题目
【题目】禽流感一直在威胁我们的生活，某疾病控制中心为了研究禽流感病毒繁殖个数
（个）随时间
（天）变化的规律，收集数据如下：
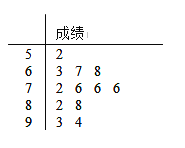
天数 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散点图可看出样本点分布在一条指数型函数
的周围.
保留小数点后两位数的参考数据：
，
，
，
，
，
，
，
，其中
（1）求出关于的回归方程（保留小数点后两位数字）；
（2）已知
，估算第四天的残差.
参考公式：
