Question

(本题满分12分)如图所示，在正方体ABCD—A1B1C1D1中， E、F分别是棱DD1 、C1D1的中点.

(1)求直线BE和平面ABB1A1所成角的正弦值；

(2)证明：B1F∥平面A1BE．

Answer 1

（1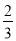） ；（2）详见解析.

【解析】

试题分析：（1）设G是AA1的中点，连接GE，BG，可证∠EBG是直线BE和平面ABB1A1所成角，而后利用直角三角形求其正弦；

（2）连接EF、AB1、C1D，记AB1与A1B的交点为H，连接EH，证明四边形B1FEH为平行四边形即可.

试题解析：【解析】
(1)设G是AA1的中点，连接GE，BG．∵E为DD1的中点，ABCD—A1B1C1D1为正方体，∴GE∥AD，又∵AD⊥平面ABB1A1，∴GE⊥平面ABB1A1，且斜线BE在平面ABB1A1内的射影为BG，∴Rt△BEG中的∠EBG是直线BE和平面ABB1A1所成角，即∠EBG=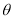．设正方体的棱长为，∴，，，

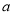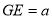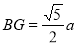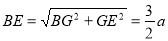∴直线BE和平面ABB1A1所成角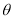的正弦值为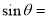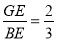：； 6分

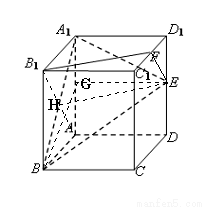
(2)证明：连接EF、AB1、C1D，记AB1与A1B的交点为H，连接EH．

∵H为AB1的中点，且B1H=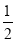C1D，B1H∥C1D，而EF=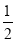C1D，EF∥C1D，

∴B1H∥EF且B1H=EF，四边形B1FEH为平行四边形，即B1F∥EH，

又∵B1F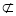平面A1BE且EH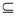平面A1BE，∴B1F∥平面A1BE． 12分

考点：1、直线与平面所成的角；2、空间直线与平面的位置关系.