题目内容
(本小题满分12分)
已知p:方程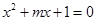 有两个不等的负根;
有两个不等的负根;
q:方程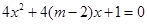 无实根.若“p或q”为真,“p且q”为假,
无实根.若“p或q”为真,“p且q”为假,
求m的取值范围.
已知p:方程
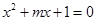 有两个不等的负根;
有两个不等的负根;q:方程
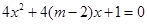 无实根.若“p或q”为真,“p且q”为假,
无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
(1)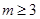 ;(2)
;(2)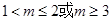 。
。
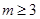 ;(2)
;(2)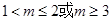 。
。本题考查的知识点是复合命题的真假,其中根据韦达定理(一元二次方程根与系数的关系)我们可以求出命题p和命题q为真是参数m的范围,是解答本题的关键.
根据韦达定理(一元二次方程根与系数的关系)我们可以求出命题p和命题q为真是参数m的范围,根据p∨q为真,p∧q为假,则p,q一真一假,构造不等式组,即可求出满足条件的m的取值范围.
.解:由已知可得
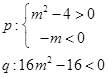 ----------------4分
----------------4分
即: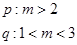 --------------6分
--------------6分
∵“p或q”为真,“p且q”为假,则p与 q中有一真一假 ---7分
(1)当p真q假时 有
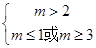 得
得 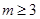 -----------------9分
-----------------9分
(2)当p假q真时 有
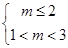 得
得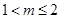 --------------11分
--------------11分
综上所求m的取值范围为: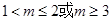 ---------12分
---------12分
根据韦达定理(一元二次方程根与系数的关系)我们可以求出命题p和命题q为真是参数m的范围,根据p∨q为真,p∧q为假,则p,q一真一假,构造不等式组,即可求出满足条件的m的取值范围.
.解:由已知可得
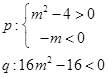 ----------------4分
----------------4分即:
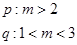 --------------6分
--------------6分∵“p或q”为真,“p且q”为假,则p与 q中有一真一假 ---7分
(1)当p真q假时 有
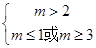 得
得 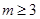 -----------------9分
-----------------9分(2)当p假q真时 有
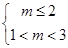 得
得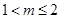 --------------11分
--------------11分综上所求m的取值范围为:
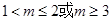 ---------12分
---------12分
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
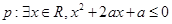 ,若命题
,若命题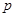 是假命题,则实数
是假命题,则实数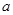 的取值范围是 .
的取值范围是 .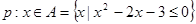
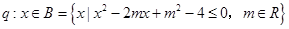 ,
,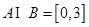 ,求实数
,求实数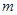 的值;
的值;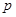 是
是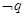 的充分条件,求实数
的充分条件,求实数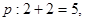
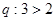 ,则下列判断中,错误的是( )
,则下列判断中,错误的是( ) 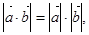 则
则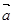 ∥
∥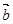 ;②
;② 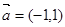 在
在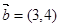 方向上的投影为
方向上的投影为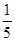 ;③若△
;③若△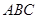 中,
中,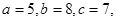 则
则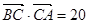 ;④若非零向量
;④若非零向量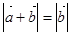 ,则
,则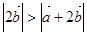 .其中所有真命题的标号是 .
.其中所有真命题的标号是 .
 ”的逆命题
”的逆命题
 ”的逆否命题
”的逆否命题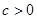 且
且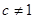 ,设
,设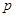 :指数函数
:指数函数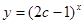 在
在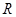 上为减函数,
上为减函数,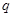 :不等式
:不等式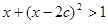 的解集为
的解集为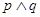 为假,
为假,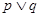 为真,求
为真,求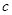 的取值范围.
的取值范围.